题目内容
5.已知抛物线y=-x2+2x+3与x轴交于A,B两点,点A在点B的左侧.(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
分析 (1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;
(2)首先求得D的坐标,然后利用面积公式即可求解.
解答 解:(1)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3.
则A的坐标是(-1,0),B的坐标是(3,0).
y=-x2+2x+3=-(x-1)2+4,
则对称轴是x=1,顶点C的坐标是(1,4);
(2)D的坐标是(1,-4).
AB=3-(-1)=4,CD=4-(-4)=8,
则四边形ACBD的面积是:$\frac{1}{2}$AB•CD=$\frac{1}{2}$×4×8=16.
点评 本题考查了待定系数法求函数解析式以及配方法确定二次函数的对称轴和顶点坐标,正确求得A和B的坐标是关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.德育处王主任将10份奖品分别放在10个完全相同的不透明礼盒中,准备将它们奖给小明等10位获“科技节活动先进个人”称号的同学.这些奖品中有5份是学习文具,3份是科普读物,2份是科技馆通票.小明同学从中随机取一份奖品,恰好取到科普读物的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
16.下列分式中,是最简分式的是( )
| A. | $\frac{xy}{x^2}$ | B. | $\frac{2}{2x-2y}$ | C. | $\frac{x+y}{{{x^2}-{y^2}}}$ | D. | $\frac{2x}{x+2}$ |
13.两个相似三角形的相似比为1:2,则它们周长的比为( )
| A. | 1:4 | B. | 1:2 | C. | $\sqrt{2}$ | D. | 4 |
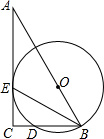 如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8.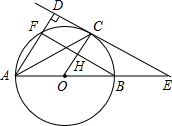 如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.
如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.