已知一次函数y=2x+b.它的图象经过另外两个函数y=-2x+1.y=x+4图象的交点.求实数b的值．题目和参考答案——青夏教育精英家教网—

题目内容

17．已知一次函数y=2x+b，它的图象经过另外两个函数y=-2x+1、y=x+4图象的交点，求实数b的值．

分析可先求出直线y=-2x+1与y=x+4图象的交点，然后把交点坐标代入y=2x+b，就可解决问题．

解答解：解$\left\{\begin{array}{l}{y=-2x+1}\\{y=x+4}\end{array}\right.$，
得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$，
把x=-1，y=3代入y=2x+b，
得b=5．

点评本题主要考查了直线上点的坐标特征、求两直线的交点坐标等知识，需要注意的是，将点的坐标转化为线段长度时，要用坐标的绝对值表示线段的长度．

练习册系列答案

相关题目

9．

如图，在正方形网格中，每个小正方形的边长均为1，三角形ABC的三个顶点恰好落在格点上．
（1）请你在图中画出点A到直线BC距离最短的线段AD，并标上字母D；
（2）直接写出三角形ABC的面积=3．

10．

如图，Rt△ABC中，∠C=90°，AC=6，BC=8．
（1）求AB的长；
（2）把△ABC沿着直线AD翻折，使得点C落在AB边上E处，求折痕AD的长．

5．

如图，已知定长线段AD=m，B、C为线段AD上的两个动点，B在C点的左侧，当B、C运动到某一位置时，AC+BD=11，AB+CD=5，求AD的长．

12．

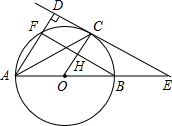如图．AB是⊙O的直径．C是⊙O上的一点．直线CE与AB的延长线相交于点E，已AD⊥CE，垂足为D．AD交⊙O于点F，AC平分∠DAE．
（1）证明：CE是⊙O的切线；
（2）连接FB交AC于H．若AB=6．AC=5，求AH的长．

2．2015年国家实施“全面二孩政策”，人民医院迎来人口出生小高峰，某天出生了3个婴儿，假设生男生女的机会相同，那么这3个婴儿中，出现1个男婴、2个女婴的概率是多少？画出树状图或列表．

9．已知a-2b=5，则2a-4b-1的值（　　）

6．当x=-3 时，分式$\frac{x-2}{x+3}$的值不存在．

7．化简：
（1）（a+2）（a-3）-（2-a）²
（2）$\frac{{{{（{x+2}）}^2}}}{{{x^2}-4}}+\frac{x+1}{x-2}-（{2-\frac{2x}{x+1}}）$．

试题分类