题目内容
2.如图,在平面直角坐标系中,已知A(16,0)、B(16,16),C(0,16),D(0,-4),点E从点A出发,以每秒1个单位的速度沿AB运动到点B停止,过点E且与AD平行的直线l与y轴相交于点F,设运动时间为t秒(t>0).(1)设t=6时,求直线l的函数表达式;
(2)若点E运动t秒后,直线l与x轴相交于点N,且CN=CE,求t的值;
(3)记EF的中点为P,请你探求线段OP随点E运动所形成的图形,说明理由并求其面积.
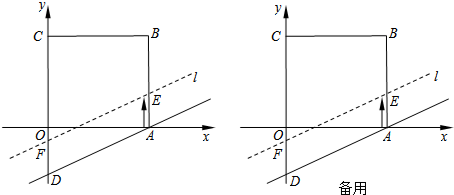
分析 (1)由t的值确定出AE的长为6,可得出直线l为直线AD向上平移6个单位,利用待定系数法确定出直线AD解析式,利用平移规律确定出直线l解析式即可;
(2)设出直线l解析式,求出直线l与x轴的交点N坐标,由CN=CE,列出关于t的方程,求出方程的解得到t的值即可;
(3)如图1所示,根据题意表示出E与F坐标,进而表示出中点P坐标,根据题意得到P点作直线运动,分别将P点的起始位置记作:P1、P2,进而得到线段OP随点E运动形成的图形为△OP1P2,求出即可.
解答 解:(1)当t=6时,AE=6,直线l可以看成直线AD向上平移了6个单位,
设直线AD的表达式为:y=kx+b,
将A(16,0)、D(0,-4)代入得:$\left\{\begin{array}{l}16k+b=0\\ b=-4\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=\frac{1}{4}\\ b=-4\end{array}\right.$,
∴直线AD的表达式为y=$\frac{1}{4}$x-4,
则此时直线l的表达式为y=$\frac{1}{4}$x+2;
(2)由题意得:0<t≤16,直线l的表达式为y=$\frac{1}{4}$x-4+t,
可得N坐标为(16-4t,0),
∵CN=CE,
∴(16-4t)2+162=162+(16-t)2,
整理得:15t2=96t,即3t(5t-32)=0,
∵t≠0,
∴t=$\frac{32}{5}$;
(3)如图1所示,
根据题意得:E(16,t)、F(0,-4+t),
则EF的中点P坐标为(8,t-2),
∴P点作直线运动,分别将P点的起始位置记作:P1、P2,
∴线段OP随点E运动形成的图形为△OP1P2,
∵0<t≤16,
∴P1(8,-2),P2(8,14),
∴P1P2=16,
则△OP1P2的面积S=$\frac{1}{2}$×16×8=64.
点评 此题属于一次函数综合题,涉及的知识有:平移规律,待定系数法求一次函数解析式,两点间的距离公式,以及三角形的面积求法,熟练掌握公式及性质是解本题的关键.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | 9 | B. | 10 | C. | 11 | D. | 无法确定 |
 如图是正方体的展开图,则原正方体相对两个面上的数字和的最大值是8.
如图是正方体的展开图,则原正方体相对两个面上的数字和的最大值是8. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8. 如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.
如图,已知定长线段AD=m,B、C为线段AD上的两个动点,B在C点的左侧,当B、C运动到某一位置时,AC+BD=11,AB+CD=5,求AD的长.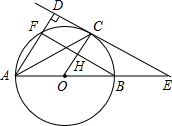 如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.
如图.AB是⊙O的直径.C是⊙O上的一点.直线CE与AB的延长线相交于点E,已AD⊥CE,垂足为D.AD交⊙O于点F,AC平分∠DAE.