题目内容
8.已知关于x的一元二次方程(k+2)x2-kx-1=0,求证:无论k为何值,方程总有两个不相等的实数根.分析 只要证明△>0即可,注意题目本身的隐含条件k≠-2.
解答 证明:∵(k+2)x2-kx-1=0是一元二次方程,
∴k≠-2,
∵△=k2+4(k+2)=(k+2)2+4,
又∵(k+2)2≥0,
∴△>0,
k≠-2时,方程总有两个不相等的实数根,
点评 本题考查根的判别式,解题的关键是记住:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )
如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )
 如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )
如图,已知反比例函数y=$\frac{k}{x}$(x>0)的图象如图所示,则k的取值范围是( )| A. | -2<k<-1 | B. | -3<k<-2 | C. | -4<k<-3 | D. | -5<k<-4 |
 已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:AC2=AD•AB.
已知,如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,求证:AC2=AD•AB.
 已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α.
已知线段a、b以及∠α,求作△ABC,使得AB+AC=a,且BC=b,∠A=∠α. 已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.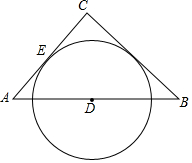 如图,△ABC中,CA=CB,D为AB的中点,以D为圆心的圆与AC相切于点E,求证:BC与⊙O相切.
如图,△ABC中,CA=CB,D为AB的中点,以D为圆心的圆与AC相切于点E,求证:BC与⊙O相切.