题目内容
20. 已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.①求证:BE=CF;
②若AF=6,BC=7,求△ABC的周长.
分析 ①连接CD,根据垂直平分线性质可得BD=CD,可证RT△BDE≌RT△CDF,可得BE=CF;
②根据Rt△ADE≌Rt△ADF得出AE=AF解答即可.
解答 ①证明:连结CD,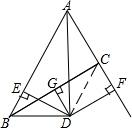 ,
,
∵D在BC的中垂线上
∴BD=CD
∵DE⊥AB,DF⊥AC
AD平分∠BAC
∴DE=DF
∠BED=∠DCF=90°
在RT△BDE和RT△CDF中,
$\left\{\begin{array}{l}{DE=DF}\\{BD=CD}\end{array}\right.$,
∴RT△BDE≌RT△CDF(HL),
∴BE=CF;
②解:由(HL)可得,Rt△ADE≌Rt△ADF,
∴AE=AF=6,
∴△ABC的周长=AB+BC+AC,
=(AE+BE)+BC+(AF-CF)
=6+7+6
=19.
点评 本题考查了直角三角形全等的判定,考查了垂直平分线的性质,考查了角平分线的性质,本题中求证RT△BDE≌RT△CDF是解题的关键.

练习册系列答案
相关题目
11.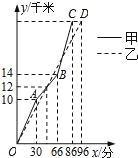 在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
 在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )
在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )| A. | 前30分钟,甲在乙的前面 | B. | 这次比赛的全程是28千米 | ||
| C. | 第48分钟时,两人第一次相遇 | D. | 甲先到达终点 |
15.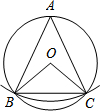 如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
 如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
9.如图,将一张三角形形纸片剪成四个小三角形,然后将其中的一个小三角形再按同样的方法剪成四个小三角形,…,如此循环进行下去.
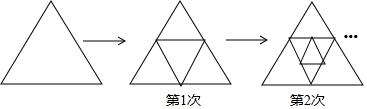
(1)填表:
(2)填空:剪n次,共剪出(3n+1)个三角形.
(3)能否经过若干次分割后共得到2016片纸片?若能,请直接写出相应的次数;若不能,请说明理由.

(1)填表:
| 次数 | 1 | 2 | 3 | 4 | … |
| 个数 | 4 | 7 | ①10 | ②13 | … |
(3)能否经过若干次分割后共得到2016片纸片?若能,请直接写出相应的次数;若不能,请说明理由.
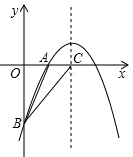 如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx-6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.