题目内容
18.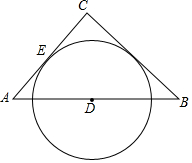 如图,△ABC中,CA=CB,D为AB的中点,以D为圆心的圆与AC相切于点E,求证:BC与⊙O相切.
如图,△ABC中,CA=CB,D为AB的中点,以D为圆心的圆与AC相切于点E,求证:BC与⊙O相切.
分析 连接ED,过点D作DF⊥BC,垂足为F,由切线的性质可知∠AED=90°,然后依据AAS证明△AED≌△BFD,从而可得到DE=DF=r,故此可证明BC是⊙D的切线.
解答 解:如图所示:连接ED,过点D作DF⊥BC,垂足为F.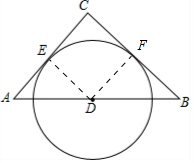
∵AC是⊙D的切线,
∴DE⊥AC.
∴∠AED=∠BFD=90°.
∵CA=CB,
∴∠A=∠B.
∵D是AB的中点,
∴AD=BD.
在△AED和△BFD中$\left\{\begin{array}{l}{∠A=∠B}\\{∠AED=∠BFD}\\{AD=BD}\end{array}\right.$,
∴△AED≌△BFD.
∴DF=DE=r.
又∵CB⊥DF,
∴CB是⊙D的切线.
点评 本题主要考查的是切线的性质和判定,掌握切线的性质和判定定理是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
9.如图,将一张三角形形纸片剪成四个小三角形,然后将其中的一个小三角形再按同样的方法剪成四个小三角形,…,如此循环进行下去.
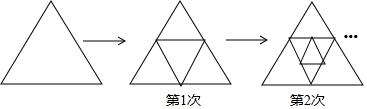
(1)填表:
(2)填空:剪n次,共剪出(3n+1)个三角形.
(3)能否经过若干次分割后共得到2016片纸片?若能,请直接写出相应的次数;若不能,请说明理由.

(1)填表:
| 次数 | 1 | 2 | 3 | 4 | … |
| 个数 | 4 | 7 | ①10 | ②13 | … |
(3)能否经过若干次分割后共得到2016片纸片?若能,请直接写出相应的次数;若不能,请说明理由.
6.单项式xm-1y3与4xyn的和是单项式,则mn的值是( )
| A. | 3 | B. | 6 | C. | 8 | D. | 9 |
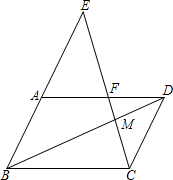 如图,在四边形ABCD中,AB∥CD,点F在边AD上,BA的延长线交CF的延长线于点E,EC交BD于点M,且CM2=EM•FM.求证:AD∥BC.
如图,在四边形ABCD中,AB∥CD,点F在边AD上,BA的延长线交CF的延长线于点E,EC交BD于点M,且CM2=EM•FM.求证:AD∥BC.