题目内容
20.某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元,若该商场同时购进甲、乙两种商品共100件恰好用去2700元.| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
(2)设甲商品购进x件,售完此两种商品总利润为y元,写出y与x的函数关系式;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销的活动.按此优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折的一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
分析 (1)设购进甲种商品m件,则购进乙种商品(100-m)件,根据同时购进甲、乙两种商品共100件恰好用去2700元即可列出关于m的一元一次方程,解之即可得出m的值,再将其代入100-m中,此题得解;
(2)设甲商品购进x件,售完此两种商品总利润为y元,则购进乙种商品(100-x)件,根据“总利润=销售单件甲种产品的利润×销售甲种产品的数量+销售单件乙种产品的利润×销售乙种产品的数量”即可得出y与x的函数关系式;
(3)根据购买件数=付款额÷甲种商品的销售单价即可求出小王购买甲种商品的件数,设小王在该商场购买乙种商品n件(n为正整数),分300<45n≤400和400<45n两种情况结合第二天只购买乙种商品打折的一次性付款324元,即可得出关于n的一元一次方程,解之即可得出结论.
解答 解:(1)设购进甲种商品m件,则购进乙种商品(100-m)件,
根据题意,得:15m+35×(100-m)=2700,
解得:m=40,
∴100-m=60.
答:购进甲种商品40件,乙种商品60件.
(2)设甲商品购进x件,售完此两种商品总利润为y元,则购进乙种商品(100-x)件,
根据题意,得:y=(20-15)x+(45-35)(100-x)=-5x+1000(0≤x≤100,且x为整数).
(3)小王在该商场购买甲种商品数量为:200÷20=10(件).
设小王在该商场购买乙种商品n件(n为正整数),
当300<45n≤400,即7≤n≤8时,有0.9×45n=324,
解得:n=8;
当400<45n,即n≥9时,有0.8×45n=324,
解得:n=9.
10+8=18(件)或10+9=19(件).
答:这两天小王在该商场购买甲、乙两种商品一共18件或19件.
点评 本题考查了一次函数的应用,根据数量关系列出一次函数关系式(算式或一元一次方程)是解题的关键.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | 0既不是整数也不是分数 | B. | 整数和分数统称有理数 | ||
| C. | 一个数的绝对值一定是正数 | D. | 绝对值等于本身的数是0和1 |
 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
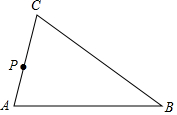 如图,在△ABC中,点P为AC上一点,请利用尺规在BC边上求作一点Q,使得△ABC∽△QPC(保留作图痕迹,不写作法)
如图,在△ABC中,点P为AC上一点,请利用尺规在BC边上求作一点Q,使得△ABC∽△QPC(保留作图痕迹,不写作法)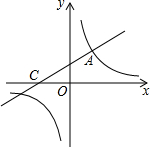 直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).
直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).