题目内容
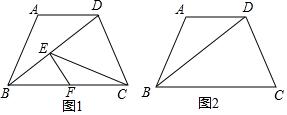
12.如图1,已知等腰△ABC中AB=AC,AD为BC边上的中线,以AB为边向外作等边△ABE,直线CE与直线AD交于点F(1)若AF=10,DF=3,试求EF的长;
(2)若以AB为边向内作等边△ABE,其它条件均不改变,请用尺规作图补全图2(保留作图痕迹),并直接写出EF、AF、DF三者的数量关系AF=2DF+EF.

分析 (1)连接BF,在FE上截取FH=BF,连接BH,易证△ABF≌△ACF,即可求得BF=CF、∠ACF=∠ABF,进而可以求证△EBH≌△ABF,即可求得EH=AF,即可求得EF的长;
(2)设∠BAD=∠CAD=α、∠ACE=∠AEC=β,得∠CAE=180°-2β、∠BAE=2α+180-2β=60°,从而知∠BAD=∠BEF,在AF上截取AG=EF,连接BG、BF,证△ABG≌△EBF得AG=EF、BG=BF,即可知△BFG为等边三角形,可得AF=AG+GF=BF+EF=2DF+EF.
解答 解:(1)连接BF,在FE上截取FH=BF,连接BH,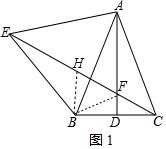
∵AB=AC,AD是BC中线,
∴∠BAD=∠CAD,
在△ABF和△ACF中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ACF(SAS),
∴BF=CF,∠ACF=∠ABF,
∵AC=AB=AE,
∴∠ACF=∠AEF,
∴∠ABF=∠AEF,
∴∠BFH=∠EAB=60°,
∴△BFH为等边三角形,∠BFC=120°,
∴∠FBH=∠EBA=60°,FC=$\frac{DF}{cos∠DFC}$=6,
∴∠ABF=∠EBH,
在△EBH和△ABF中,
∵$\left\{\begin{array}{l}{EB=AB}\\{∠ABF=∠EBH}\\{HB=FB}\end{array}\right.$,
∴△EBH≌△ABF(SAS),
∴EH=AF=10,
∴EF=EH+HF=AF+FC=16;
(2)AF=2DF+EF,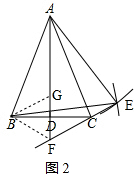
∵△ABE为等边三角形,AB=AC,
∴AE=AB=AC,
设∠BAD=∠CAD=α,∠ACE=∠AEC=β,
∴∠CAE=180°-2β,
∴∠BAE=2α+180-2β=60°,
∴∠BAD=∠BEF,
在AF上截取AG=EF,连接BG、BF,
在△ABG和△EBF中,
∵$\left\{\begin{array}{l}{AB=EB}\\{∠BAG=∠BEF}\\{AG=EF}\end{array}\right.$,
∴△ABG≌△EBF(SAS),
∴AG=EF,BG=BF,
∴△BFG为等边三角形,
∴AF=AG+GF=BF+EF=2DF+EF,
故答案为:AF=2DF+EF.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABF≌△ACF和△EBH≌△ABF是解题的关键.

| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
(2)设甲商品购进x件,售完此两种商品总利润为y元,写出y与x的函数关系式;
(3)在“五•一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销的活动.按此优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折的一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
 如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).
如图,在平面直角坐标系内,已知点A(2,2),B(-6,-4),C(2,-4).
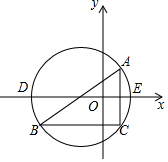
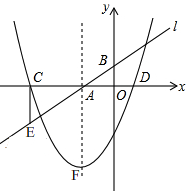 如图1,直线l:y=mx+n交x轴,y轴于点A,B,抛物线与x轴交于点C、D,对称轴经过点A,顶点F的纵坐标为-3.CE⊥x轴交直线l于点E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.
如图1,直线l:y=mx+n交x轴,y轴于点A,B,抛物线与x轴交于点C、D,对称轴经过点A,顶点F的纵坐标为-3.CE⊥x轴交直线l于点E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.