题目内容
 如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF.
如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF. (1)求证:∠EDF=45°;
(2)当AB=3AE=3,求EF的长.
考点:翻折变换(折叠问题),正方形的性质
专题:
分析:(1)作DG⊥EF于G,根据折叠的性质可知∠ADE=∠GDE,∠CDF=∠GDF,由正方形的性质可得∠ADC=90°,依此即可求解;
(2)根据AB=3AE=3,可知AE=1,BE=2,根据折叠的性质可知EG=AE=1,FG=FC,设BF=x,则EF=3-x+1,在Rt△BEF中,根据勾股定理即可求解.
(2)根据AB=3AE=3,可知AE=1,BE=2,根据折叠的性质可知EG=AE=1,FG=FC,设BF=x,则EF=3-x+1,在Rt△BEF中,根据勾股定理即可求解.
解答: (1)证明:作DG⊥EF于G.
(1)证明:作DG⊥EF于G.
由折叠的性质可知∠ADE=∠GDE,∠CDF=∠GDF,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴∠EDF=
∠ADC=45°;
(2)解:∵AB=3AE=3,
∴AE=1,BE=2,
由折叠的性质可知EG=AE=1,FG=FC,
设BF=x,则EF=3-x+1=4-x,
在Rt△BEF中,(4-x)2=22+x2,
解得x=1.5,
则EF=4-x=2.5.
 (1)证明:作DG⊥EF于G.
(1)证明:作DG⊥EF于G.由折叠的性质可知∠ADE=∠GDE,∠CDF=∠GDF,
∵四边形ABCD是正方形,
∴∠ADC=90°,
∴∠EDF=
| 1 |
| 2 |
(2)解:∵AB=3AE=3,
∴AE=1,BE=2,
由折叠的性质可知EG=AE=1,FG=FC,
设BF=x,则EF=3-x+1=4-x,
在Rt△BEF中,(4-x)2=22+x2,
解得x=1.5,
则EF=4-x=2.5.
点评:本题考查了翻折变换问题;由翻折得到相等的角和线段,利用勾股定理是正确解答本题的关键.

练习册系列答案
相关题目
 如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于D、E,AB=1,则cos∠C等于( )
如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于D、E,AB=1,则cos∠C等于( )| A、DE | B、AC | C、CE | D、BC |
 如图,已知直线
如图,已知直线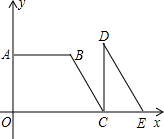 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-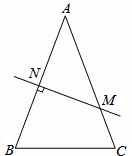 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2.-2).
在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2.-2). 如图,正方形ABCD中,AB=4,点E是BC的中点,点P是对角线AC上一动点(点P与点A、C不重合),则在点P的移动过程中,△PBE周长的最小值是
如图,正方形ABCD中,AB=4,点E是BC的中点,点P是对角线AC上一动点(点P与点A、C不重合),则在点P的移动过程中,△PBE周长的最小值是