题目内容
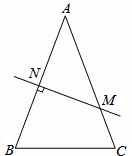 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.(1)若∠B=70°,则∠NMA的度数是
(2)探究∠B与∠NMA的关系,并说明理由;
(3)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使PB+CP的值最小?若存在,标出点P的位置并求PB+CP的最小值;若不存在,说明理由.
考点:轴对称-最短路线问题,线段垂直平分线的性质,等腰三角形的性质
专题:
分析:(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
(2)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(3)根据垂直平分线的性质,可得AM与MB的关系,再根据三角形的周长,可得答案;根据两点之间线段最短,可得P点与M点的关系,可得PB+PC与AC的关系.
解答:解:(1)若∠B=70°,则∠NMA的度数是 50°,
故答案为:50°;
(2)猜想的结论为:∠NMA=2∠B-90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°-2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°-∠A=90°-(180°-2∠B)=2∠B-90°.
(3)如图:

①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14 cm,
∴AC+BC=14 cm,
∴BC=6 cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
故答案为:50°;
(2)猜想的结论为:∠NMA=2∠B-90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°-2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°-∠A=90°-(180°-2∠B)=2∠B-90°.
(3)如图:

①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14 cm,
∴AC+BC=14 cm,
∴BC=6 cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
点评:本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等得出PB=PA.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△ABC中,CD是边AB上的高,且CD2=AD•DB,求证:∠ACB=90°.
如图,△ABC中,CD是边AB上的高,且CD2=AD•DB,求证:∠ACB=90°.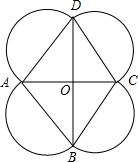 如图是一个花圃培育基地的平面图,此花圃培育基地内部的四边形ABCD是一个平行四边形,花圃周围是分别由边AB,BC,CD,DA为直径的四个半圆,这四个半圆和?ABCD的对角线AC,BD都是通道,已知通道AC与BD相交于点O,经测量得知∠ADC=60°,BC=7cm,OA=3.5m,茗茗从点B出发以顺时针方向沿半圆通道运动,墨墨同时从点D出发以逆时针方向沿半圆通道运动,若茗茗运动的路程s(m)与时间t(s)满足关系:s=
如图是一个花圃培育基地的平面图,此花圃培育基地内部的四边形ABCD是一个平行四边形,花圃周围是分别由边AB,BC,CD,DA为直径的四个半圆,这四个半圆和?ABCD的对角线AC,BD都是通道,已知通道AC与BD相交于点O,经测量得知∠ADC=60°,BC=7cm,OA=3.5m,茗茗从点B出发以顺时针方向沿半圆通道运动,墨墨同时从点D出发以逆时针方向沿半圆通道运动,若茗茗运动的路程s(m)与时间t(s)满足关系:s= 如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF.
如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF.  已知:如图,在△ABC中,DE∥BC,AD=AE,BE平分∠ABC.求证:DE=EC.
已知:如图,在△ABC中,DE∥BC,AD=AE,BE平分∠ABC.求证:DE=EC. 如图,直线y=
如图,直线y= 如图,在平面直角坐标系中,已知A、B是y=
如图,在平面直角坐标系中,已知A、B是y=