题目内容
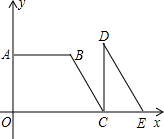 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-| 2 |
| 3 |
| 4 |
| 3 |
(1)求四边形OABC的面积S0;
(2)设CE=t,试将S表示为t的函数,并求S=2时t的值.
考点:二次函数综合题
专题:
分析:(1)当x=0时求出A点坐标,根据A点纵坐标求出B点纵坐标,令函数值为0,求出C点横坐标;
(2)根据题意分三种情况讨论:
①当CD=2CE=2t≤OA=2,即t≤1时,公共部分的最大区域为△CDE;
②当CD>OA且CE<OC,即1<t<3时,延长AB交CD于F、交DE于G,公共部分的最大区域为梯形CFGE;
③当CE≥OC,即t≥3时,公共部分的最大区域为梯形OABC.
(2)根据题意分三种情况讨论:
①当CD=2CE=2t≤OA=2,即t≤1时,公共部分的最大区域为△CDE;
②当CD>OA且CE<OC,即1<t<3时,延长AB交CD于F、交DE于G,公共部分的最大区域为梯形CFGE;
③当CE≥OC,即t≥3时,公共部分的最大区域为梯形OABC.
解答:解:(1)x=0时,y=-
x+
x+2=2,可得,A(0,2);
解-
x+
x+2=2,得,x=0(舍去)或x=2,可得,B(2,2);
解-
x+
x+2=0得,x=-1(舍去)或x=3,可得,C(3,0);
∴A(0,2)、B(2,2)、C(3,0),
S0=
(AB+OC)OA=5;
(2)∵BC∥DE,
∴
=
=2,即CD=2CE=2t,
①当CD=2CE=2t≤OA=2,即t≤1时,公共部分的最大区域为△CDE,
∴S=S△CDE=
t•2t=t2;
②当CD>OA且CE<OC,即1<t<3时,延长AB交CD于F、交DE于G,公共部分的最大区域为梯形CFGE,
∴S=S四边形CFGE=
(CE+FG)CF=
[t+(t-1)]×2=2t-1;
③当CE≥OC,即t≥3时,公共部分的最大区域为梯形OABC,
∴S=S0=5;
当S=2时,由以上函数关系式知,S=2t-1=2,此时t=
.
| 2 |
| 3 |
| 4 |
| 3 |
解-
| 2 |
| 3 |
| 4 |
| 3 |
解-
| 2 |
| 3 |
| 4 |
| 3 |
∴A(0,2)、B(2,2)、C(3,0),
S0=
| 1 |
| 2 |
(2)∵BC∥DE,
∴
| CD |
| CE |
| OA |
| OC-AB |
①当CD=2CE=2t≤OA=2,即t≤1时,公共部分的最大区域为△CDE,
∴S=S△CDE=
| 1 |
| 2 |
②当CD>OA且CE<OC,即1<t<3时,延长AB交CD于F、交DE于G,公共部分的最大区域为梯形CFGE,
∴S=S四边形CFGE=
| 1 |
| 2 |
| 1 |
| 2 |
③当CE≥OC,即t≥3时,公共部分的最大区域为梯形OABC,
∴S=S0=5;
当S=2时,由以上函数关系式知,S=2t-1=2,此时t=
| 3 |
| 2 |
点评:本题考查了二次函数综合题,利用图形找到最大面积,再进行计算.要进行分类讨论,注意各取值范围.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

 如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:
如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论: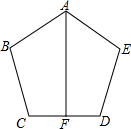 如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点.
如图,已知AB=AE,∠B=∠E,BC=ED,F是边CD的中点. 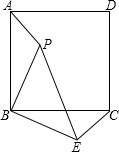 已知:点P是正方形内一点,△ABP旋转后能与△CBE重合.
已知:点P是正方形内一点,△ABP旋转后能与△CBE重合. 如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF.
如图,E、F分别是正方形ABCD的边AB、BC上的点,将△ADE、△CDF分别沿DE,DF折叠,恰好得到△DEF.  如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足