题目内容
17．先化简，再求值：[（x-y）2+（x+y）（x-y）]÷2x，其中$x=\sqrt{2}$，$y=3+\sqrt{2}$．分析 原式中括号中利用完全平方公式及平方差公式化简，再利用多项式除以单项式法则计算得到最简结果，把x与y的值代入计算即可求出值．
解答 解：原式=（x2-2xy+y2+x2-y2）÷2x=（2x2-2xy）÷2x=x-y，
当x=$\sqrt{2}$，y=3+$\sqrt{2}$时，原式=$\sqrt{2}$-3-$\sqrt{2}$=-3．
点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，点A、D、C、E在同一条直线上，AB∥EF，AB=EF，AD=EC，AE=10，AC=6，则CD的长为2．
5．下列图形：
其中是轴对称图形的共有（ ）
其中是轴对称图形的共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．若$\sqrt{x-1}$和$\sqrt{1-x}$在实数范围内都有意义，则x的取值是（ ）
| A． | x≥1 | B． | x≤1 | C． | x=1 | D． | -1≤x≤1 |
2．我们学习了整式的乘法后，可进行如下计算：（a+b）1=a+b；（a+b）2=a2+2ab+b2；（a+b）3=（a+b）2（a+b）=a3+3a2b+3ab2+b3；
…
如果我们对（a+b）n （n取正整数）的计算结果中各项系数进一步研究，可以列出下表：
上表称为“杨辉三角”，揭示了二项式乘方展开式的规律．
（1）请仔细观察表中的规律，写出（a+b）4展开式中所缺的系数：（a+b）4=a4+a3b+a2b2+ab3+b4
（2）请写出（a+b）5的展开式：（a+b）5=（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
（3）当n=1、2、3、4、…时，（a+b）n展开式的第三项系数分别为0、1、3、6、…，猜想（a+b）n展开式的第三项系数为$\frac{n（n-1）}{2}$（用含n的代数式表示）；
（4）当n=1、2、3、4、…时，（a+b）n展开式的各项系数之和分别为2、4、8、16、…，猜想（a+b）n展开式的各项系数之和为2n（用含n的代数式表示）．
…
如果我们对（a+b）n （n取正整数）的计算结果中各项系数进一步研究，可以列出下表：
| （a+b）1=a+b | 1 | 1 | ||||||||
| （a+b）2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| （a+b）3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| … | … |
（1）请仔细观察表中的规律，写出（a+b）4展开式中所缺的系数：（a+b）4=a4+a3b+a2b2+ab3+b4
（2）请写出（a+b）5的展开式：（a+b）5=（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
（3）当n=1、2、3、4、…时，（a+b）n展开式的第三项系数分别为0、1、3、6、…，猜想（a+b）n展开式的第三项系数为$\frac{n（n-1）}{2}$（用含n的代数式表示）；
（4）当n=1、2、3、4、…时，（a+b）n展开式的各项系数之和分别为2、4、8、16、…，猜想（a+b）n展开式的各项系数之和为2n（用含n的代数式表示）．
6．
如图，∠C=90°，AM平分∠CAB，CM=20cm，那么M到AB的距离是（ ）
如图，∠C=90°，AM平分∠CAB，CM=20cm，那么M到AB的距离是（ ）| A． | 10cm | B． | 15cm | C． | 20cm | D． | 25cm |
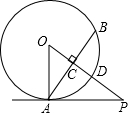如图，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA=2，OP=4，则弦AB的长2$\sqrt{3}$．