��Ŀ����
2������ѧϰ����ʽ�ij˷��ɽ������¼��㣺��a+b��1=a+b����a+b��2=a2+2ab+b2����a+b��3=��a+b��2��a+b��=a3+3a2b+3ab2+b3����
������Ƕԣ�a+b��n ��nȡ���������ļ������и���ϵ����һ���о��������г��±���
| ��a+b��1=a+b | 1 | 1 | ||||||||
| ��a+b��2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| ��a+b��3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| �� | �� |
��1������ϸ�۲���еĹ��ɣ�д����a+b��4չ��ʽ����ȱ��ϵ������a+b��4=a4+a3b+a2b2+ab3+b4
��2����д����a+b��5��չ��ʽ����a+b��5=��a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
��3����n=1��2��3��4����ʱ����a+b��nչ��ʽ�ĵ�����ϵ���ֱ�Ϊ0��1��3��6���������루a+b��nչ��ʽ�ĵ�����ϵ��Ϊ$\frac{n��n-1��}{2}$���ú�n�Ĵ���ʽ��ʾ����
��4����n=1��2��3��4����ʱ����a+b��nչ��ʽ�ĸ���ϵ��֮�ͷֱ�Ϊ2��4��8��16���������루a+b��nչ��ʽ�ĸ���ϵ��֮��Ϊ2n���ú�n�Ĵ���ʽ��ʾ����
���� ��1�����ݡ�������ǡ���ϵ������ȷ��������ϵ�����ɣ�
��2�����ݡ�������ǡ���ϵ������ȷ��������չ��ʽ���ɣ�
��3�����ݡ�������ǡ���ϵ������ȷ��������ϵ��������õ�������ɣ�
��4�����ݡ�������ǡ���ϵ������ȷ��������ϵ���������ϵ��֮�ͼ��ɣ�
��� �⣺��1����a+b��4չ��ʽ����ȱ��ϵ������a+b��4=a4+4a3b+6a2b2+4ab3+b4��
��2����a+b��5��չ��ʽ����a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5��
��3����n=1��2��3��4����ʱ����a+b��nչ��ʽ�ĵ�����ϵ���ֱ�Ϊ 0��1��3��6���������루a+b��nչ��ʽ�ĵ�����ϵ��Ϊ$\frac{n��n-1��}{2}$��
��4����n=1��2��3��4����ʱ����a+b��nչ��ʽ�ĸ���ϵ��֮�ͷֱ�Ϊ2��4��8��16���������루a+b��nչ��ʽ�ĸ���ϵ��֮��Ϊ2n��
�ʴ�Ϊ����2����a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5����3��0��1��3��6��$\frac{n��n-1��}{2}$����4��2��4��8��16��2n
���� ���⿼������ʽ�Ļ�����㣬Ū�塰������ǡ���ϵ�������ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
�����Ŀ
12�� ��ͼ����֪A��B��C�����ڡ�O�ϣ���C���ӻ�AB�ϣ��ҡ�AOB=130�㣬���ACB�Ķ���Ϊ��������
��ͼ����֪A��B��C�����ڡ�O�ϣ���C���ӻ�AB�ϣ��ҡ�AOB=130�㣬���ACB�Ķ���Ϊ��������
 ��ͼ����֪A��B��C�����ڡ�O�ϣ���C���ӻ�AB�ϣ��ҡ�AOB=130�㣬���ACB�Ķ���Ϊ��������
��ͼ����֪A��B��C�����ڡ�O�ϣ���C���ӻ�AB�ϣ��ҡ�AOB=130�㣬���ACB�Ķ���Ϊ��������| A�� | 130�� | B�� | 125�� | C�� | 120�� | D�� | 115�� |
10����a+3b����3b-a����ȷ�ļ������ǣ�������
| A�� | 9b2-a2 | B�� | a2-3b2 | C�� | a2-9b2 | D�� | a2+9b2 |
11�� ��ͼ������ABCD�У�AB=4��BC=8���ѡ�BCD�ضԽ���BD���۵õ���BC��D������AC�䣬���߶�AC��ij���Ϊ��������
��ͼ������ABCD�У�AB=4��BC=8���ѡ�BCD�ضԽ���BD���۵õ���BC��D������AC�䣬���߶�AC��ij���Ϊ��������
 ��ͼ������ABCD�У�AB=4��BC=8���ѡ�BCD�ضԽ���BD���۵õ���BC��D������AC�䣬���߶�AC��ij���Ϊ��������
��ͼ������ABCD�У�AB=4��BC=8���ѡ�BCD�ضԽ���BD���۵õ���BC��D������AC�䣬���߶�AC��ij���Ϊ��������| A�� | $\frac{12}{5}$ | B�� | 4 | C�� | $\frac{12\sqrt{5}}{5}$ | D�� | 2$\sqrt{5}$ |
 ��͡�Ķ���ʱ�����ˣ��ݱ�����2015��11��26�գ��ӣ��ݣ��𣨽������ң���·���������нΣ����ݵ����ң��˿����г����г�ԼΪ290km��������ͨ�������г�ԼΪ250km������ʱ��ȿ����г����õ�ʱ�������2.375h����������ƽ���ٶ��ǿ����г�ƽ���ٶȵ�2.5��������ƽ���ٶȣ�
��͡�Ķ���ʱ�����ˣ��ݱ�����2015��11��26�գ��ӣ��ݣ��𣨽������ң���·���������нΣ����ݵ����ң��˿����г����г�ԼΪ290km��������ͨ�������г�ԼΪ250km������ʱ��ȿ����г����õ�ʱ�������2.375h����������ƽ���ٶ��ǿ����г�ƽ���ٶȵ�2.5��������ƽ���ٶȣ�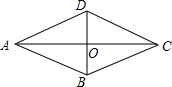 һ�����ε�һ���Խ��߳�60cm���ܳ���200cm����
һ�����ε�һ���Խ��߳�60cm���ܳ���200cm����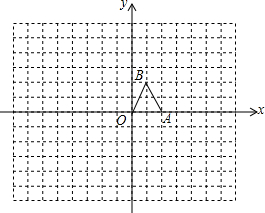 ��ͼ���ڱ߳���Ϊ1��С����������ֽ�У���OAB�Ķ���O��A��B���ڸ���ϣ���O��ֱ������ϵ��ԭ�㣬��A��x���ϣ���OΪλ�����ģ�����OAB�Ŵ�ʹ�÷Ŵ��ġ�OA1B1���OAB��Ӧ�߶εı�Ϊ2��1��������OA1B1����д����Ӧ�ĵ�A1��B1�����꣮������һ��������ɣ�
��ͼ���ڱ߳���Ϊ1��С����������ֽ�У���OAB�Ķ���O��A��B���ڸ���ϣ���O��ֱ������ϵ��ԭ�㣬��A��x���ϣ���OΪλ�����ģ�����OAB�Ŵ�ʹ�÷Ŵ��ġ�OA1B1���OAB��Ӧ�߶εı�Ϊ2��1��������OA1B1����д����Ӧ�ĵ�A1��B1�����꣮������һ��������ɣ�