题目内容
7.在平面直角坐标中标出下列各点A(5,1),B(5,0),C(2,1),D(2,3)并顺次连接,求出所得图形的面积.分析 建立平面直角坐标系,根据已给四点坐标确定出点A、B、C、D的位置,再顺次连接即可,再利用割补法求四边形的面积,计算即可得解.
解答 解:在平面直角坐标系中各点的位置如图所示: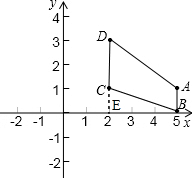
延长DC交x轴与点E,则E(2,0)
故S四边形ABCD=S梯形ABED-S△BCE
=$\frac{1}{2}$×(AB+DE)×BE-$\frac{1}{2}$×BE×CE
=$\frac{1}{2}$×(1+3)×3-$\frac{1}{2}$×3×1
=$\frac{9}{2}$,
故所求四边形ABCD的面积为$\frac{9}{2}$.
点评 本题考查了坐标与图形性质、割补法求四边形的面积,熟练掌握在平面直角坐标系中确定点的位置的方法是解题的前提,割补法求面积是常用方法.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
15.甲厂和乙厂都有某种仪器可供其他厂使用,其中甲厂可提供10台,乙厂可提供4台,已知丙厂需要8台,丁厂需要6台,从甲厂到丙厂、丁厂每台仪器需运费分别为400元和800元,乙厂到丙厂、丁厂每台仪器的运费分别为300元和500元.设甲厂运往丙厂的仪器为x台.
(1)请用含x的代数式填写下表中的空格:
(2)现计划用7600元运送这批仪器,请你设计一种调运方案,使丙厂、丁厂能得到所需的仪器,而且费用正好用完;
(3)试问有无可能使总运费为8000元?若可能,请求出甲厂运往丙厂的仪器台数;若不可能,请说明理由.
(1)请用含x的代数式填写下表中的空格:
| 起点/终点 | 丙厂 | 丁厂 |
| 甲厂 | x | 10-x |
| 乙厂 | 8-x | x-4 |
(3)试问有无可能使总运费为8000元?若可能,请求出甲厂运往丙厂的仪器台数;若不可能,请说明理由.
12. 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
 如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )
如图.已知A、B、C三点在⊙O上,点C在劣弧AB上,且∠AOB=130°,则∠ACB的度数为( )| A. | 130° | B. | 125° | C. | 120° | D. | 115° |
16.如图的各组图形中,相似的是( )


| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (1)(3)(4) | D. | (1)(2)(4) |
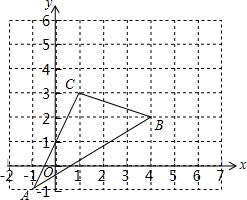 如图,三角形ABC在平面直角坐标系中,将三角形ABC向左平移1个单位长度,再向上平移3个单位长度得到△A1B1C1,;
如图,三角形ABC在平面直角坐标系中,将三角形ABC向左平移1个单位长度,再向上平移3个单位长度得到△A1B1C1,;