题目内容
7.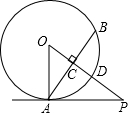 如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长2$\sqrt{3}$.
如图,PA与⊙O相切于点A,弦AB⊥OP,垂足为C,OP与⊙O相交于点D,已知OA=2,OP=4,则弦AB的长2$\sqrt{3}$.
分析 由已知条件可知Rt△POA中,OP=2OA,所以可求出∠P=30°,∠O=60°,再在Rt△AOC中,利用勾股定理求解直角三角形即可得到AB的长.
解答 解:∵PA与⊙O相切于点A,
∴OA⊥AP,
∴三角形△POA是直角三角形,
∵OA=2,OP=4,即OP=2OA,
∴∠P=30°,∠O=60°,
则在Rt△AOC中,OC=$\frac{1}{2}$OA=1,则AC=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 本题主要考查了切线的性质以及勾股定理的运用,能够熟练运用勾股定理的性质求解一些简单的直角三角形是中考常见题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
19.已知m-n=-2,则代数式10-m+n=( )
| A. | 8 | B. | 12 | C. | -8 | D. | -12 |
 如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.
如图,点B的坐标(4,4),过点B作BA⊥x轴,垂足为A,作BC⊥y轴,垂足为C,反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,其交点为M,连接AM.求证:AM=AO.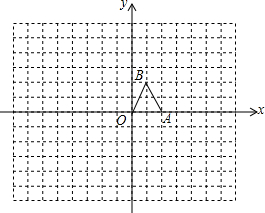 如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1,并写出相应的点A1、B1的坐标.(画出一种情况即可)
如图,在边长均为1的小正方形网格纸中,△OAB的顶点O、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2:1,画出△OA1B1,并写出相应的点A1、B1的坐标.(画出一种情况即可)
 如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.
如图,点M,N在线段AC上,AM=CN,AB∥CD,AB=CD,试说明∠1=∠2.