题目内容
13.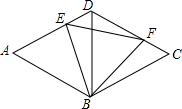 如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.
如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)试探索在点E,F滑动过程中,△DEF的面积是否存在最大值?如果存在,求出这个值,如果不存在,说明理由.
分析 (1)由菱形的性质得DA=DC=AB=BC=4,加上BD=4,则可判断△ABD和△BDC都是等边三角形,所以∠EDB=∠C=60°,再利用AE+CF=4可得DE=CF,于是根据“SAS”可判断△BDE≌△BCF;
(2)根据全等三角形的性质得BE=BF,∠DBE=∠FBC,由于∠DBF+∠FBC=∠DBC=60°,所以∠DBF+∠DBE=60°,于是可判断△BEF为等边三角形;
(3)根据等边三角形的面积公式得到S△BEF=$\frac{\sqrt{3}}{4}$BE2,由点E,F均不与点A,C,D重合)得到BE有最小值,没有最大值,于是判断△DEF的面积不存在最大值.
解答 (1)证明:∵四边形ABCD为菱形,
∴DA=DC=AB=BC=4,
而BD=4,
∴△ABD和△BDC都是等边三角形,
∴∠EDB=∠C=60°,
∵AE+CF=4,
而AE+DE=AD=4,
∴DE=CF,
在△BDE和△BCF中
$\left\{\begin{array}{l}{DE=CF}\\{∠EDB=∠FCB}\\{DB=CB}\end{array}\right.$,
∴△BDE≌△BCF;
(2)解:△BEF为等边三角形.理由如下:
∵△BDE≌△BCF,
∴BE=BF,∠DBE=∠FBC,
∵∠DBF+∠FBC=∠DBC=60°,
∴∠DBF+∠DBE=60°,
∴△BEF为等边三角形;
(3)解:不存在.
∵在点E,F滑动过程中,△DEF为等边三角形,
∴S△BEF=$\frac{\sqrt{3}}{4}$BE2,
∵点E,F均不与点A,C,D重合),
∴BE有最小值,没有最大值,
∴△DEF的面积不存在最大值.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了等边三角形的判定与性质和三角形全等的判定与性质.

 名校课堂系列答案
名校课堂系列答案 某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:| 原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
| 螺丝 | a | 1.0 | 2.0 |
| 螺母 | a-0.3 | 0.6 |
(1)求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,要求两种配件的总量不超过3000个,且螺母的数量不少于500个.
①设购进螺丝x个,求x的取值范围;
②该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?
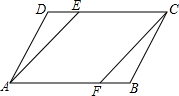 如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF.
如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF.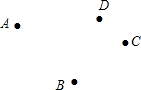 已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.
已知平面上A、B、C、D四个点,请用直尺按下列步骤要求完成画图.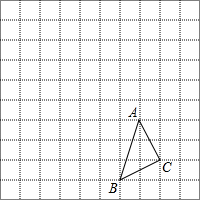 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.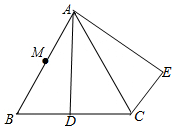 如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.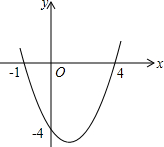 二次函数y=ax2+bx+c的图象如图所示,求:
二次函数y=ax2+bx+c的图象如图所示,求: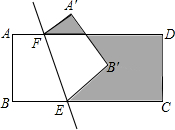 如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.
如图,矩形ABCD中,AB=2cm,BC=5cm,将四边形ABEF沿直线EF折叠,点A落在A′处,点B落在B′处,则阴影部分的周长为14cm.