题目内容
8.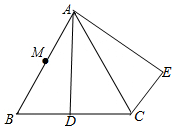 如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.(1)旋转中心是点A,∠DAE=60°;
(2)如果M是AB的中点,那么经过上述旋转后,点M转到了AC的中点位置,并在图中用点M′标出来;
(3)如果BD=$\frac{1}{3}$BC,且△ABD的面积为3,那么△ADC的面积为6.
分析 (1)根据等边三角形的性质得∠BAC=60°,再根据旋转的性质得旋转中心是点A,∠DAE=∠BAC=60°;
(2)利用对应关系确定M′点的位置;
(3)根据三角形面积公式求解.
解答 解:(1)∵△ABC为等边三角形,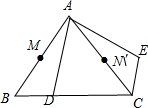
∴∠BAC=60°
∵△ABD绕点A逆时针旋转到△ACE的位置,
∴旋转中心是点A,∠DAE=∠BAC=60°;
(2)∵AB和AC为对应边,
∴经过上述旋转后,点M转到了AC的中点位置,如图,
(3)∵BD=$\frac{1}{3}$BC,
∴CD=2BD,
∴S△ADC=2S△ABD=2×3=6.
故答案为点A,60;AC的中点;6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了三角形面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.不等式-x2+2x+3>0的解为( )
| A. | -1<x<3 | B. | x>3或x<-1 | C. | -3<x<1 | D. | x>1或x<-3 |
18.下列各式分解因式正确的是( )
| A. | $\frac{1}{2}$-2a2=$\frac{1}{2}$(1+2a)(1-2a) | B. | x2+4y2=(x+2y)2 | ||
| C. | x2-3x+9=(x-3)2 | D. | x2-y2=(x-y)2 |
 如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长.
如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长. 如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.
如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.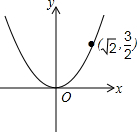 如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).
如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).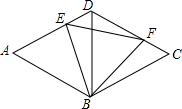 如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.
如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.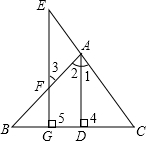 已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由. 如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=39°,∠B=129°.
如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=39°,∠B=129°.