题目内容
18. 某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:| 原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
| 螺丝 | a | 1.0 | 2.0 |
| 螺母 | a-0.3 | 0.6 |
(1)求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,要求两种配件的总量不超过3000个,且螺母的数量不少于500个.
①设购进螺丝x个,求x的取值范围;
②该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?
分析 (1)依据用40元购进螺丝的数量与用16元购进螺母的数量相同可建立关于a的分式方程,解答出即可;
(2)①设购进螺丝x个,则购进螺母(3x+200)个,根据两种配件的总量不超过3000个,且螺母的数量不少于500个,可建立一元一次不等式组,求解即可;
②设当购进螺丝x个时的总利润为y元,建立关于利润的函数关系式,根据x的取值范围,解答出即可.
解答 解:(1)依题意,得$\frac{40}{a}$=$\frac{16}{a-0.3}$,
解得,a=0.5,
经检验,a=0.5是原方程的解,且符合题意;
(2)①设购进螺丝x个,则购进螺母(3x+200)个,
依题意,得:$\left\{\begin{array}{l}{x+3x+200≤3000}\\{3x+200≥500}\end{array}\right.$,
解得,100≤x≤700,
即x的取值范围是100≤x≤700;
②设当购进螺丝x个时的总利润为y元,
则y=(2.0-0.5-0.2×2)×$\frac{1}{2}$x+(1.0-0.5)×$\frac{1}{2}$x+(0.6-0.2)×(2x+200)=1.6x+80,
∵k=1.6>0,y随x的增大而增大,又由①知100≤x≤700,
∴当x=700时,y最大=1.6×700+80=1200,此时3x+200=2300;
∴该采购员应该购进螺丝700个,螺母2300个,才能获得最大利润;最大利润是1200元.
点评 本题考查了一次函数、一元一次不等式及分式方程的应用,注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目
3.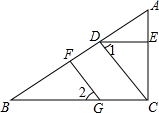 如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;(5)∠BFG=∠BDC.
 如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;(5)∠BFG=∠BDC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7. 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
 一个包装盒的表面展开图如图所示,包装盒的容积为750cm3,请写出关于x的方程15x(30-2x)÷2=750,化成一般形式是x2-15x+50=0.
一个包装盒的表面展开图如图所示,包装盒的容积为750cm3,请写出关于x的方程15x(30-2x)÷2=750,化成一般形式是x2-15x+50=0. 如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.
如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.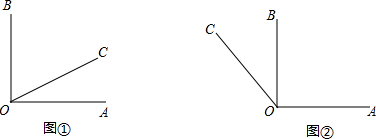
 如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.
如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.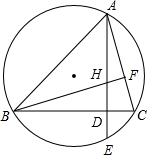 如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.
如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E. 如图,△ABC是等边三角形,过点C作CD⊥CB交∠CBA的外角平分线于点D,连结AD,过点C作∠BCE=∠BAD交AB的延长线于点E.
如图,△ABC是等边三角形,过点C作CD⊥CB交∠CBA的外角平分线于点D,连结AD,过点C作∠BCE=∠BAD交AB的延长线于点E.