题目内容
1.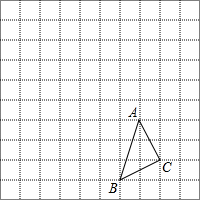 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.(1)请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,-1)、B(1,-4).并求出C点的坐标;
(2)作出△ABC关于横轴对称的△A1B1C1,再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2,并写出C1、C2两点的坐标.
分析 (1)利用点A和点B的坐标建立直角坐标系,然后写出C点坐标;
(2)利用关于x轴对称的点的坐标特征写出点A、B、C的对应点A1、B1、C1的坐标,在描点即可得到△A1B1C1;利用利用原点对称的点的坐标特征,写出点A、B、C的对应点A2、B2、C2的坐标,然后描点即可得到△A2B2C2.
解答 解:(1) 如图,C点坐标为(3,-3);
如图,C点坐标为(3,-3);
(2)如图,△A1B1C1、△A2B2C2为所作,C1、C2两点的坐标分别为(3,3)、(-3,3).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.不等式-x2+2x+3>0的解为( )
| A. | -1<x<3 | B. | x>3或x<-1 | C. | -3<x<1 | D. | x>1或x<-3 |
 如图,B是AC边上一点,AD∥BE,∠1=∠2,求证:∠A=∠E.
如图,B是AC边上一点,AD∥BE,∠1=∠2,求证:∠A=∠E.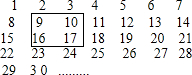 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表. 如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.
如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.
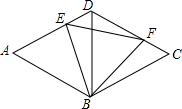 如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.
如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.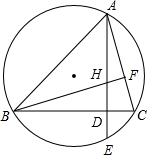 如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.
如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E. 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE.
如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:OB=OE.