题目内容
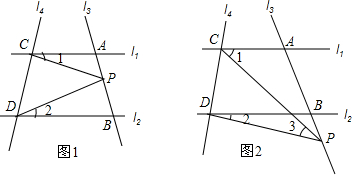
19.如图1,已知直线l1平行l2,且l3与l1、l2分别交于A、B两点,l4与l1、l2分别交于C、D两点,点P在直线AB上.(1)当点P在A、B两点之间时,试猜想∠CPD与∠1、∠2的数量关系,并说明理由.
(2)如果点P在A、B两点之间运动时,问∠CPD与∠1、∠2的关系是否发生变化?
(3)如果点P在A、B两点外侧运动(如图2)时,试探究∠CPD与∠1、∠2的关系(点P和A、B不重合),并写出探究过程.
分析 (1)延长CP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(2)延长CP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(3)结论:∠3=∠1-∠2.BD与PC相交于点N,根据平行线得出∠1=∠CND,根据三角形外角性质求出即可.
解答 解:(1)∠CPD=∠1+∠2,延长CP交直线l2于E,如图1:
∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠CPD=∠DEC+∠2,
∴∠CPD=∠1+∠2;
(2)不变,
理由是:∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠CPD=∠DEC+∠2,
∴∠CPD=∠1+∠2;
(3)结论:∠3=∠1-∠2.理由如下:
设BD与PC相交于N,如图2:
∵AC∥BD,
∴∠1=∠CND,
∵∠CND=∠2+∠3,
∴∠1=∠2+∠3,
∴∠3=∠1-∠2.
点评 本题考查了平行线性质的应用,主要根据学生的推理能力,用了运动观点进行分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.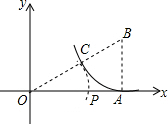 如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
 如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )
如图,Rt△OAB的直角边OA长为2,直角边AB长为1,OA在数轴上,在OB上截取BC=BA,以原点O为圆心,OC的长为半径画弧,交正半轴于一点P,则OP中点对应的实数是( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{3}-1$ |
14.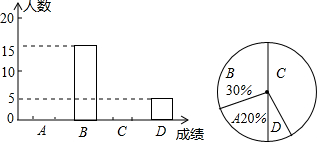 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
请根据以上所提供的信息回答下列问题:
(1)统计表中的m=10,n=20,并补全条形统计图;
(2)若该校九年级有1000名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名;
(3)针对学生在学习中存在的问题,老师对学生进行了一段时间的针对性复习与训练,若A级学生数可提高40%,B级学生数可提高10%,请估计经过训练后九年级数学成绩在B以上(含B级)的学生可达多少名.
 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:请根据以上所提供的信息回答下列问题:
| 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
(2)若该校九年级有1000名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名;
(3)针对学生在学习中存在的问题,老师对学生进行了一段时间的针对性复习与训练,若A级学生数可提高40%,B级学生数可提高10%,请估计经过训练后九年级数学成绩在B以上(含B级)的学生可达多少名.
11. 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )
 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
8. 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
 如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )
如图,△ABC中,∠A=40°,点D为延长线上一点,且∠CBD=120°,则∠C=( )| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
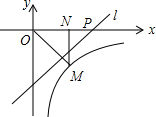 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$. 如图所示,等腰直角△ABC中,M、N为斜边AB上两点,且∠MCN=45°,求证:以AM、MN、BN三边为边长构成的三角形是直角三角形.
如图所示,等腰直角△ABC中,M、N为斜边AB上两点,且∠MCN=45°,求证:以AM、MN、BN三边为边长构成的三角形是直角三角形. 如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=87°.
如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A=87°.