题目内容
4.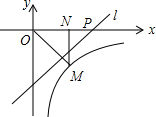 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点M(1,-1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=$\frac{1+\sqrt{5}}{2}$.
分析 根据反比例函数图象上点的坐标特征由点A坐标为(1,-1)得到k=-1,即反比例函数解析式为y=-$\frac{1}{x}$,且ON=MN=1,则可判断△OMN为等腰直角三角形,知∠MON=45°,再利用PQ⊥OM可得到∠OPQ=45°,然后轴对称的性质得PN=PN′,NN′⊥PQ,所以∠NPQ=∠N′PQ=45°,于是得到N′P⊥x轴,则点n′的坐标可表示为(t,-$\frac{1}{t}$),于是利用Pn=Pn′得t-1=|-$\frac{1}{t}$|=$\frac{1}{t}$,然后解方程可得到满足条件的t的值.
解答 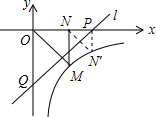 解:如图,∵点M坐标为(1,-1),
解:如图,∵点M坐标为(1,-1),
∴k=-1×1=-1,
∴反比例函数解析式为y=-$\frac{1}{x}$,
∵ON=MN=1,
∴△OMN为等腰直角三角形,
∴∠MON=45°,
∵直线l⊥OM,
∴∠OPQ=45°,
∵点N和点N′关于直线l对称,
∴PN=PN′,NN′⊥PQ,
∴∠N′PQ=∠OPQ=45°,∠N′PN=90°,
∴N′P⊥x轴,
∴点N′的坐标为(t,-$\frac{1}{t}$),
∵PN=PN′,
∴t-1=|-$\frac{1}{t}$|=$\frac{1}{t}$,
整理得t2-t-1=0,解得t1=$\frac{1+\sqrt{5}}{2}$,t2=$\frac{1-\sqrt{5}}{2}$(不符合题意,舍去),
∴t的值为$\frac{1+\sqrt{5}}{2}$.
故答案为:$\frac{1+\sqrt{5}}{2}$.
点评 本题考查了反比例函数的综合题,涉及知识点有反比例函数图象上点的坐标特征、等腰直角三角形的性质和轴对称的性质和用求根公式法解一元二次方程等.利用对称的性质得到关于t的方程是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
14.若一批学生的年龄(单位:岁)分别是14,15,16,16,17,17,则这批学生年龄的中位数是( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
12. 如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )
如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )
 如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )
如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG的度数为( )| A. | 35° | B. | 40° | C. | 70° | D. | 140° |
9.比-2015小1的数是( )
| A. | -2014 | B. | 2014 | C. | -2016 | D. | 2016 |
16.(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为(1,4),点C的坐标为(0,3).
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
| x | … | -2 | -1 | 1 | 2 | 4 | 5 | … |
| y1 | … | -5 | 0 | 4 | 3 | -5 | -12 | … |
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=-3时,y2=12.
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.
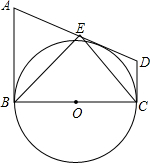 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,以BC为直径的⊙O与AD相切,点E为AD的中点,下列结论正确的个数是( )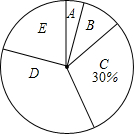 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题: