��Ŀ����
11�� ��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��E��FΪ�߶�AB�������㣬�ҡ�ECF=45�㣬����E��F�ֱ���BC��AC�Ĵ����ཻ�ڵ�M������ֱ�ΪH��G���������½��ۣ���AB=$\sqrt{2}$���ڵ���E���B�غ�ʱ��MH=$\frac{1}{2}$����AF+BE=EF����MG•MH=$\frac{1}{2}$��������ȷ����Ϊ��������
��ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC=1��E��FΪ�߶�AB�������㣬�ҡ�ECF=45�㣬����E��F�ֱ���BC��AC�Ĵ����ཻ�ڵ�M������ֱ�ΪH��G���������½��ۣ���AB=$\sqrt{2}$���ڵ���E���B�غ�ʱ��MH=$\frac{1}{2}$����AF+BE=EF����MG•MH=$\frac{1}{2}$��������ȷ����Ϊ��������| A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
���� ��������֪����ABC�ǵ���ֱ�������Σ����ݵ���ֱ�������μ��������жϣ�
����ͼ1������E���B�غ�ʱ����H���B�غϣ��ɵ�MG��BC���ı���MGCB�Ǿ��Σ���һ���õ�FG�ǡ�ACB����λ�ߣ��Ӷ������жϣ�
����ͼ2��ʾ��SAS��֤��ECF�ա�ECD������ȫ�������ε����ʺ��ɶ������������жϣ�
�ܸ���AA��֤��ACE�ס�BFC���������������ε����ʿɵ�AF•BF=AC•BC=1��������֪�ı���CHMG�Ǿ��Σ��ٸ���ƽ���ߵ����ʺ͵��������õ�MG•MH=$\frac{\sqrt{2}}{2}$AE��$\frac{\sqrt{2}}{2}$BF=$\frac{1}{2}$AE•BF=$\frac{1}{2}$AC•BC=$\frac{1}{2}$�����˼��������жϣ�
��� �⣺��������֪����ABC�ǵ���ֱ�������Σ�
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2}$���ʢ���ȷ��
����ͼ1������E���B�غ�ʱ����H���B�غϣ�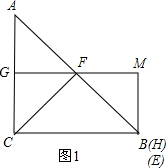
��MB��BC����MBC=90�㣬
��MG��AC��
���MGC=90��=��C=��MBC��
��MG��BC���ı���MGCB�Ǿ��Σ�
��MH=MB=CG��
�ߡ�FCE=45��=��ABC����A=��ACF=45�㣬
��CF=AF=BF��
��FG�ǡ�ACB����λ�ߣ�
��GC=$\frac{1}{2}$AC=MH���ʢ���ȷ��
����ͼ2��ʾ��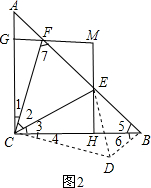
��AC=BC����ACB=90�㣬
���A=��5=45�㣮
����ACF˳ʱ����ת90������BCD��
��CF=CD����1=��4����A=��6=45�㣻BD=AF��
�ߡ�2=45�㣬
���1+��3=��3+��4=45�㣬
���DCE=��2��
�ڡ�ECF�͡�ECD�У�
$\left\{\begin{array}{l}{CF=CD}\\{��2=��DCE}\\{CE=CE}\end{array}\right.$��
���ECF�ա�ECD��SAS����
��EF=DE��
�ߡ�5=45�㣬
���DBE=90�㣬
��DE2=BD2+BE2����EF2=AF2+BE2���ʢ۴���
�ܡߡ�7=��1+��A=��1+45��=��1+��2=��ACE��
�ߡ�A=��5=45�㣬
���ACE�ס�BFC��
��$\frac{AE}{BC}$=$\frac{AC}{BF}$��
��AE•BF=AC•BC=1��
������֪�ı���CHMG�Ǿ��Σ�
��MG��BC��MH=CG��
MG=CH��MH��AC��
��$\frac{CH}{BC}$=$\frac{AE}{AB}$��$\frac{CG}{AC}$=$\frac{BF}{AB}$��
��$\frac{MG}{1}$=$\frac{AE}{\sqrt{2}}$��$\frac{MH}{1}$=$\frac{BF}{\sqrt{2}}$��
��MG=$\frac{\sqrt{2}}{2}$AE��MH=$\frac{\sqrt{2}}{2}$BF��
��MG•MH=$\frac{\sqrt{2}}{2}$AE��$\frac{\sqrt{2}}{2}$BF=$\frac{1}{2}$AE•BF=$\frac{1}{2}$AC•BC=$\frac{1}{2}$��
�ʢ���ȷ��
��ѡ��C��
���� �������������ۺ��⣬�漰��֪ʶ���У�����ֱ�������ε��ж������ʣ�ƽ���ߵ��ж������ʣ����ε��ж������ʣ���������λ�ߵ����ʣ�ȫ�������ε��ж������ʣ����ɶ��������������ε��ж������ʣ��ۺ��Խ�ǿ����һ�����Ѷȣ�

| x | �� | -2 | -1 | 1 | 2 | 4 | 5 | �� |
| y1 | �� | -5 | 0 | 4 | 3 | -5 | -12 | �� |
��2������������m1��x�ᷭ�ۣ��õ�������m2��y2=a2x2+b2x+c2����x=-3ʱ��y2=12��
��3���ڣ�1���������£���������m1��ˮƽ����ƽ�ƣ��õ�������m3����������m1��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��������m3��x�ύ��M��N���㣨��M�ڵ�N����ࣩ������C��ƽ����x���ֱ�ߣ���������m3�ڵ�K���ʣ��Ƿ������A��C��K��MΪ������ı��������ε����Σ������ڣ��������K�����ꣻ�������ڣ���˵�����ɣ�
 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ��ٷ���ax2+bx+c=0������֮�ʹ���0�� ��a+b��0����y��x�����������a-b+c��0����2a-b��0�� ������ȷ�ĸ�����������
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ��ٷ���ax2+bx+c=0������֮�ʹ���0�� ��a+b��0����y��x�����������a-b+c��0����2a-b��0�� ������ȷ�ĸ�����������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
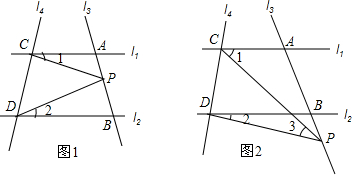
 ��ͼ����֪D��E�ֱ��ڡ�ABC�ı�AB��AC�ϣ�DΪAB���е㣬AE��EC=2��1����ADE�ס�ACB���ҡ�ADE=��C����$\frac{DE}{BC}$��ֵ��
��ͼ����֪D��E�ֱ��ڡ�ABC�ı�AB��AC�ϣ�DΪAB���е㣬AE��EC=2��1����ADE�ס�ACB���ҡ�ADE=��C����$\frac{DE}{BC}$��ֵ�� ��ͼ��ij�����˶�Ավ�ڵ�O����ϰ���ţ�������������0.5m��A�����������߳�����A��y���ϣ�������ķ��и߶�y����λ��m�������ʱ��t����λ��s��֮�����㺯����ϵy=at2+5t+c����֪�������0.8sʱ�������ĸ߶�Ϊ3.5m��
��ͼ��ij�����˶�Ավ�ڵ�O����ϰ���ţ�������������0.5m��A�����������߳�����A��y���ϣ�������ķ��и߶�y����λ��m�������ʱ��t����λ��s��֮�����㺯����ϵy=at2+5t+c����֪�������0.8sʱ�������ĸ߶�Ϊ3.5m�� ��ͼ����ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{6}$x2+bx+c����A��0��4����C��8��0����P��t��0����x���������ϵ�һ�����㣬M���߶�AP���е㣬���߶�MP�Ƶ�P˳ʱ����ת90����߶�PB������B��x��Ĵ��ߣ�����A��y��Ĵ��ߣ���ֱ�߽��ڵ�D��
��ͼ����ƽ��ֱ������ϵxOy�У�������y=-$\frac{1}{6}$x2+bx+c����A��0��4����C��8��0����P��t��0����x���������ϵ�һ�����㣬M���߶�AP���е㣬���߶�MP�Ƶ�P˳ʱ����ת90����߶�PB������B��x��Ĵ��ߣ�����A��y��Ĵ��ߣ���ֱ�߽��ڵ�D��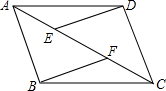 ��ͼ����?ABCD�У�E��FΪ�Խ���AC�ϵ����㣬��AE=CF������DE��BF��
��ͼ����?ABCD�У�E��FΪ�Խ���AC�ϵ����㣬��AE=CF������DE��BF��