题目内容
6.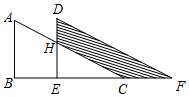 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.
分析 易证△ABC∽△HEC,根据相似三角形的对应边的比相等,即可求得EC的长,则可以求得△DEF与△HEC的面积,两者的面积的差就是所求的阴影部分的面积.
解答 解:∵AB∥HE,
∴△ABC∽△HEC,
∴$\frac{EC}{BC}$=$\frac{HE}{AB}$=$\frac{7}{10}$,
∴设EC=x,则BC=6+x,则 $\frac{x}{6+x}=\frac{7}{10}$,
解得:x=14.
∴BC=6+14=20.
∴S△ABC=S△DEF=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×10×20=100,
S△HEC=$\frac{1}{2}$HE•EC=$\frac{1}{2}$×7×20=70.
∴阴影部分的面积为S△DEF-S△HEC=100-70=30.
故答案是:30.
点评 本题考查了相似三角形的判定与性质,利用相似三角形的对应边的比相等,正确求得EC的长度是关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
18. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°
④BC+FG=1.5,其中正确的结论是( )
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°
④BC+FG=1.5,其中正确的结论是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ② |
15.若甲数为x,乙数为y,则“甲数的3倍比乙数的一半少2”列成方程是( )
| A. | 3x+$\frac{1}{2}$y=2 | B. | 3x-$\frac{1}{2}$y=2 | C. | -3x+$\frac{1}{2}$y=2 | D. | 3x=$\frac{1}{2}$y+2 |
 △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.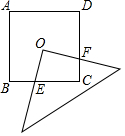 如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2.
如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2. 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B2017的坐标是(22016,22017-1).
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B2017的坐标是(22016,22017-1). 如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.
如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.