题目内容
1.已知n边形的对角线共有$\frac{n(n-3)}{2}$条(n是不小于3的整数);(1)五边形的对角线共有5条;
(2)若n边形的对角线共有35条,求边数n;
(3)若n边形的边数增加1,对角线总数增加9,求边数n.
分析 (1)把n=5代入$\frac{n(n-3)}{2}$即可求得五边形的对角线的条数;
(2)根据题意得$\frac{n(n-3)}{2}$=35求得n值即可;
(3)$\frac{(n+1)(n+1-3)}{2}$-$\frac{n(n-3)}{2}$=9,求得n的值即可.
解答 解:(1)当n=5时,$\frac{n(n-3)}{2}$=$\frac{5×2}{2}$=5,
故答案为:5.
(2)$\frac{n(n-3)}{2}$=35,
整理得:n2-3n-70=0,
解得:n=10或n=-7(舍去),
所以边数n=10.
(3)根据题意得:$\frac{(n+1)(n+1-3)}{2}$-$\frac{n(n-3)}{2}$=9,
解得:n=10.
所以边数n=10.
点评 本题考查了多边形的对角线的知识,了解多边形的对角线的计算方法是解答本题的关键,难度不大.

练习册系列答案
相关题目
9. 如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )
如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )
 如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )
如图,点A、B、C、D在⊙O上,BC是⊙O的直径,若∠D=36°,则∠BCA的度数是( )| A. | 54° | B. | 72° | C. | 45° | D. | 36° |

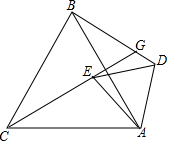 如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.
如图,△ABC、△ADE都是等边三角形,点G为射线BD,CE的交点.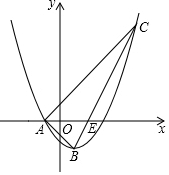 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.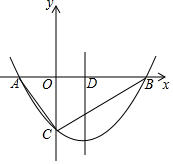 定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.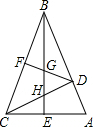 已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.
已知:如图,在△ABC中,BC=BA,BE平分∠CBA交边CA于点E,∠ABC=45°,CD⊥AB,垂足为D,F为BC中点,BE与DF、DC分别交于点G、H.