题目内容
13.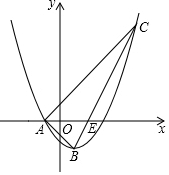 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.(1)求抛物线的表达式及点E的坐标;
(2)联结AB,求∠B的正切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
分析 (1)由对称轴可求得a的值,再把A点坐标代入可求得c的值,则可求得抛物线表达式,则可求得B、C的坐标,由待定系数法可求得直线BC的解析式,可求得E点坐标;
(2)由A、B、C三点的坐标可求得AB、AC和BC的长,可判定△ABC是以BC为斜边的直角三角形,利用三角形的定义可求得答案;
(3)设M(x,0),当∠GCM=∠BAE时,可知△AMC为等腰直角三角形,可求得M点的坐标;当∠CMG=∠BAE时,可证得△MEC∽△MCA,利用相似三角形的性质可求得x的值,可求得M点的坐标.
解答 解:
(1)∵抛物线对称轴为x=1,
∴-$\frac{-1}{2a}$=1,解得a=$\frac{1}{2}$,
把A点坐标代入可得$\frac{1}{2}$+1+c=0,解得c=-$\frac{3}{2}$,
∴抛物线表达式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
∵y=$\frac{1}{2}$x2-x-$\frac{3}{2}$=$\frac{1}{2}$(x-1)2-2,
∴B(1,-2),
把C(5,m)代入抛物线解析式可得m=$\frac{25}{2}$-5-$\frac{3}{2}$=6,
∴C(5,6),
设直线BC解析式为y=kx+b,
把B、C坐标代入可得$\left\{\begin{array}{l}{k+b=-2}\\{5k+b=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$,
∴直线BC解析式为y=2x-4,
令y=2可得2x-4=0,解得x=2,
∴E(2,0);
(2)∵A(-1,0),B(1,-2),C(5,6),
∴AB=2$\sqrt{2}$,AC=$\sqrt{(5+1)^{2}+{6}^{2}}$=6$\sqrt{2}$,BC=$\sqrt{(5-1)^{2}+(6+2)^{2}}$=4$\sqrt{5}$,
∴AB2+AC2=8+72=80=BC2,
∴△ABC是以BC为斜边的直角三角形,
∴tan∠B=$\frac{AC}{AB}$=$\frac{6\sqrt{2}}{2\sqrt{2}}$=3;
(3)∵A(-1,0),B(1,-2),
∴∠CAE=∠BAE=45°,
∵GM⊥BC,
∴∠CGM+∠GCB=∠GCB+∠ABC=90°,
∴∠CGM=∠ABC,
∴当△CGM与△ABE相似时有两种情况,
设M(x,0),则C(x,2x-4),
①当∠GCM=∠BAE=45°时,则∠AMC=90°,
∴MC=AM,即2x-4=x+1,解得x=5,
∴M(5,0);
②当∠GMC=∠BAE=∠MAC=45°时,
∵∠MEC=∠AEB=∠MCG,
∴△MEC∽△MCA,
∴$\frac{ME}{MC}$=$\frac{MC}{MA}$,即$\frac{x-2}{MC}$=$\frac{MC}{x+1}$,
∴MC2=(x-2)(x+1),
∵C(5,6),
∴MC2=(x-5)2+62=x2-10x+61,
∴(x-2)(x+1)=x2-10x+61,解得x=7,
∴M(7,0);
综上可知M点的坐标为(5,0)或(7,0).
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、勾股定理及其逆定理、三角函数的定义、相似三角形的判定和性质、方程思想及分类讨论思想等知识.在(1)中注意利用对称轴求得a的值是解题的关键,在(2)中证得△ABC为直角三角形是解题的关键,在(3)中利用相似三角形的性质得到关于M点坐标的方程是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度适中.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | a>1 | B. | a≤1 | C. | a≥1 | D. | a<1 |
| A. | (4,-2) | B. | (-4,2) | C. | (-2,-4) | D. | (2,4) |
| A. | 图象经过(1,-1) | B. | 图象位于二、四象限 | ||
| C. | 图象是中心对称图形 | D. | y随x的增大而减小 |
| A. | 4 | B. | 2 | C. | 8 | D. | 6 |
| A. | 1500m | B. | 4500m | C. | 3700m | D. | 5500m |
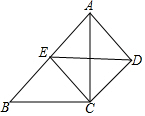 如图,CD∥AB,且CD=$\frac{1}{2}$AB,点E为AB的中点,若四边形ADCE为正方形,则∠B=45°.
如图,CD∥AB,且CD=$\frac{1}{2}$AB,点E为AB的中点,若四边形ADCE为正方形,则∠B=45°.