题目内容
12.已知△ABC内接于⊙O,过点A作直线EF.(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī)EF⊥AB (īī)∠BAE=90°(īīī)∠ABC=∠EAC
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

分析 (1)根据切线的判断由AB⊥EF或∠BAE=90°可判断EF为⊙O的切线;
当∠ABC=∠EAC,根据圆周角定理得∠ABC+∠CAB=90°,所以∠EAC+∠CAB=90°,即AB⊥EF,于是也可判断EF为⊙O的切线;
(2)作直径AD,连结CD,由AD为直径得∠ACD=90°,则∠D+∠CAD=90°,根据圆周角定理得∠D=∠B,而∠CAE=∠B,所以∠CAE=∠D,则∠EAC+∠CAD=90°,根据切线的判定定理得到EF为⊙O的切线;
解答 (1)解:如图1中,当AB⊥EF或∠BAE=90°可判断EF为⊙O的切线;
当∠ABC=∠EAC,∵AB为直径,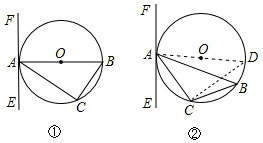
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF为⊙O的切线;
故答案为AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
(2)证明:如图2,作直径AD,连结CD,
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠D=∠B,∠CAE=∠B,
∴∠CAE=∠D,
∴∠EAC+∠CAD=90°,
∴AD⊥EF,
∴EF为⊙O的切线;
点评 本题考查了圆周角定理,切线的判定的应用,主要考查学生运用定理进行推理的能力,注意:经过半径的外端,并且垂直于半径的直线是圆的切线.

练习册系列答案
相关题目
3.关于x的不等式组$\left\{\begin{array}{l}x>a\\ x>2-a\end{array}\right.$的解集是x>a,则a的取值范围是( )
| A. | a>1 | B. | a≤1 | C. | a≥1 | D. | a<1 |
20.下列各组数中,互为相反数的是( )
| A. | 2与$\frac{1}{2}$ | B. | -1与(-1)2 | C. | (-1)2与1 | D. | 2与|-2| |
7.下列合并同类项中正确的是( )
| A. | 5xy-xy=5 | B. | m+m=m2 | C. | -y-y=0 | D. | -2xy+2xy=0 |
4.若二次函数y=ax2的图象经过点P(-2,4),则该图象必经过点( )
| A. | (4,-2) | B. | (-4,2) | C. | (-2,-4) | D. | (2,4) |