题目内容

9．已知x=$\frac{\sqrt{5}-1}{2}$，y=$\frac{\sqrt{5}+1}{2}$，则x2+y2-xy的值是2．

分析 先求出x+y和xy的值，再根据完全平方公式进行变形，最后代入求出即可．

解答 解：∵x=$\frac{\sqrt{5}-1}{2}$，y=$\frac{\sqrt{5}+1}{2}$，
∴x+y=$\frac{\sqrt{5}-1}{2}$+$\frac{\sqrt{5}+1}{2}$=$\sqrt{5}$，xy=$\frac{\sqrt{5}-1}{2}$×$\frac{\sqrt{5}+1}{2}$=1，
∴x2+y2-xy=（x+y）2-3xy=（$\sqrt{5}$）2-3×1=2，
故答案为：2．

点评 本题考查了二次根式的化简求出值，完全平方公式等知识点，能正确根据完全平方公式进行变形是解此题的关键．

练习册系列答案
相关题目
19．[发现]如图∠ACB=∠ADB=90°，那么点D在经过A，B，C三点的圆上（如图①）

[思考]如图②，如果∠ACB=∠ADB=a（a≠90°）（点C，D在AB的同侧），那么点D还在经过A，B，C三点的⊙O上吗？
我们知道，如果点D不在经过A，B，C三点的圆上，那么点D要么在⊙O外，要么在⊙O内，以下该同学的想法说明了点D不在⊙O外．请结合图④证明点D也不在⊙O内．
【证】
[结论]综上可得结论，如果∠ACB=∠ADB=α（点C，D在AB的同侧），那么点D在经过A，B，C三点的圆上，即：A、B、C、D四点共圆．
[应用]利用上述结论解决问题：
如图⑤，已知△ABC中，∠C=90°，将△ACB绕点A顺时针旋转α度（α为锐角）得△ADE，连接BE、CD，延长CD交BE于点F；
（1）用含α的代数式表示∠ACD的度数；
（2）求证：点B、C、A、F四点共圆；
（3）求证：点F为BE的中点．
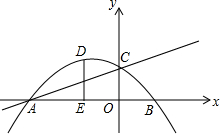20．如图，抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A（-3，0），C（0，1）两点．
（1）直线的表达式为y=$\frac{1}{3}$x+1；抛物线的表达式为y=-$\frac{1}{3}$x2-$\frac{2}{3}$x+1．
（2）D为抛物线在第二象限部分上的一点，作DE垂直x轴于点E，交直线AC于点F，求线段DF长度的最大值，并求此时点D的坐标；
（3）P为抛物线上一动点，且P在第四象限内，过点P作PN垂直x轴于点N，使得以P、A、N为顶点的三角形与△ACO相似，请直接写出点P的坐标．
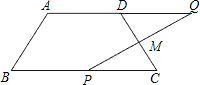17．如图，在四边形ABCD中，AD∥BC，AD=5cm，BC=9cm．M是CD的中点，P是BC边上的一动点（P与B，C不重合），连接PM并延长交AD的延长线于Q．
（1）试说明△PCM≌△QDM．
（2）当点P在点B、C之间运动到什么位置时，四边形ABPQ是平行四边形？并说明理由．
4．（1）计算：$\sqrt{4}$+20170-|$\sqrt{3}$-2|+1
（2）计算：$\frac{{x}^{2}+4x+4}{{x}^{2}+2x}$÷（2x-$\frac{4+{x}^{2}}{x}$）
14．如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．
（1）尝试探究：
结论1：DM、MN的数量关系是DM=MN；
结论2：DM、MN的位置关系是DM⊥MN；
（2）猜想论证：证明你的结论．
（3）拓展：如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，（1）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．
1．如图，AB为⊙O直径，点C，D为⊙O上两点，若∠C+∠AOD=145°，则∠C的大小是（　　）
A．30°B．35°C．40°D．45°
18．下列运算正确的是（　　）
A．x2+x3=x5B．（x-2）2=x2-4C．（x3）4=x7D．2x2?x3=2x5
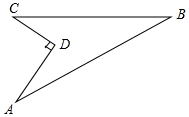8．如图，已知AD=4，CD=3，BC=12，AB=13，∠ADC=90°，求四边形ABCD的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网