题目内容
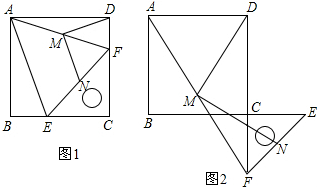
14.如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.(1)尝试探究:
结论1:DM、MN的数量关系是DM=MN;
结论2:DM、MN的位置关系是DM⊥MN;
(2)猜想论证:证明你的结论.
(3)拓展:如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,(1)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
分析 (1)写出结论1和2;
(2)结论1,根据三角形中位线得:MN=$\frac{1}{2}AE$,根据直角三角形斜边中线得:DM=$\frac{1}{2}$AF,证明△ABE≌△ADF可以得出结论;
结论2:主要证明∠NMD=∠BAD=90°即可;
(3)连接AE,交MD于点G,标记出各个角,首先证明出MN∥AE,MN=$\frac{1}{2}$AE,再有(1)的结论以及角角之间的数量关系得到∠DMN=∠DGE=90°.
解答 解:(1)结论1:DM、MN的数量关系是:DM=MN,
结论2:DM、MN的位置关系是:DM⊥MN,
故答案为:DM=MN,DM⊥MN;
(2)结论1:DM=MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN=$\frac{1}{2}$AE,
∵四边形ABCD是正方形,
∴∠ADF=∠B=90°,AB=AD=BC=CD,
∴DM=$\frac{1}{2}$AF,
∵△ECF是等腰直角三角形,
∴EC=FC,
∴BE=DF,
在△ABE和△ADF中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠ADF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∴DM=MN;
结论2,DM、MN的位置关系是:DM⊥MN,理由是:
如图1,∵M是AF的中点,N是EF的中点,
∴MN∥AE,
∴∠NMF=∠EAF,
∵△ABE≌△ADF,
∴∠BAE=∠FAD,
Rt△ADF中,∵M是AF的中点,
∴AM=DM,
∴∠FAD=∠MDA,
∵∠FMD=∠FAD+∠MDA=∠FAD+∠BAE,
∴∠DMN=∠NMF+∠FMD=∠EAF+∠BAE+∠FAD=90°,
∴DM⊥MN;
(3)(2)中的两个结论还成立,
证明:连接AE,交MD于点G,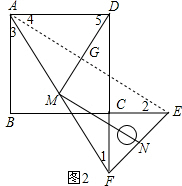
∵点M为AF的中点,点N为EF的中点,
∴MN∥AE,MN=$\frac{1}{2}$AE,
由(1)同理可证,
AB=AD=BC=CD,∠B=∠ADF,CE=CF,
又∵BC+CE=CD+CF,即BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
在Rt△ADF中,
∵点M为AF的中点,
∴DM=$\frac{1}{2}$AF,
∴DM=MN,
∵△ABE≌△ADF,
∴∠1=∠2,
∵AB∥DF,
∴∠1=∠3,
同理可证:∠2=∠4,
∴∠3=∠4,
∵DM=AM,
∴∠MAD=∠5,
∴∠DGE=∠5+∠4=∠MAD+∠3=90°,
∵MN∥AE,
∴∠DMN=∠DGE=90°,
∴DM⊥MN.
点评 本题主要考查正方形的性质以及全等三角形的判定与性质等知识点,解答本题的关键是利用好各小题之间的联系,此题难度不大,但是角与角之间的数量关系有点复杂,请同学们解答的时候注意.

| A. | 3 | B. | -2 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
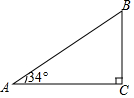 如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米)
如图,某山坡坡长AB为110米,坡角(∠A)为34°,求坡高BC及坡宽AC.(结果精确到0.1米)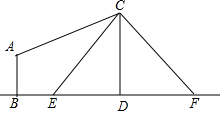 如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.
如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=$\sqrt{3}$米,BE=3米,求拉线CE的长.

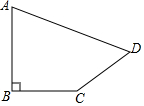 如图所示,在四边形ABCD中,∠B=90°,AB=2,BC=CD=1,AD=$\sqrt{6}$,试求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠B=90°,AB=2,BC=CD=1,AD=$\sqrt{6}$,试求四边形ABCD的面积.