题目内容
13.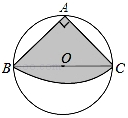 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
| A. | 12cm | B. | 20cm | C. | 24cm | D. | 28cm |
分析 设这块圆形纸片的半径为R,圆锥的底面圆的半径为r,利用等腰直径三角形的性质得到AB=$\sqrt{2}$R,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到2πr=$\frac{90•π•\sqrt{2}R}{180}$,解得r=$\frac{\sqrt{2}}{4}$R,然后利用勾股定理得到($\sqrt{2}$R)2=(3$\sqrt{30}$)2+($\frac{\sqrt{2}}{4}$R)2,再解方程求出R即可得到这块圆形纸片的直径.
解答 解:设这块圆形纸片的半径为R,圆锥的底面圆的半径为r,则AB=$\sqrt{2}$R,
根据题意得2πr=$\frac{90•π•\sqrt{2}R}{180}$,解得r=$\frac{\sqrt{2}}{4}$R,
所以($\sqrt{2}$R)2=(3$\sqrt{30}$)2+($\frac{\sqrt{2}}{4}$R)2,解得R=12,
所以这块圆形纸片的直径为24cm.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.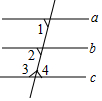 如图,下列推理错误的是( )
如图,下列推理错误的是( )
 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
1.4cos60°的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
8. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
18.两名同学都进行了5次立定跳远测试.经计算,他们的平均成绩相同,若要比较这两名同学的成绩谁更稳定,通常还需要比较他们成绩的( )
| A. | 众数 | B. | 中位数 | C. | 方差 | D. | 以上都不对 |
5.在-2.5,$\frac{1}{3}$,0,2这四个数中,最小的数是( )
| A. | -2.5 | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |
 如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.
如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F. 如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.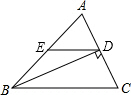 如图:在△ABC中,D是AC的中点,且BD⊥AC,ED∥BC,ED交AB于点E,BC=5cm,AC=4cm,求△AED的周长.
如图:在△ABC中,D是AC的中点,且BD⊥AC,ED∥BC,ED交AB于点E,BC=5cm,AC=4cm,求△AED的周长.