题目内容
2. 如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.
如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4$\sqrt{3}$,求菱形ABCD的面积.
分析 (1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形;
(2)欲求菱形ABCD的面积,已知AC=4$\sqrt{3}$,只需求得BD的长度即可.利用平行四边形以及菱形的性质可得AC⊥CE,再解直角△ACE求出CE的长度,即为BD的长度.则利用菱形ABCD的面积等于两对角线乘积的一半即可求解.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形; (2)解:∵四边形BECD是平行四边形,
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠E=∠OBA,
∴AC⊥CE.
在直角△ACE中,∵∠E=60°,AC=4$\sqrt{3}$,
∴CE=$\frac{AC}{tan∠E}$=$\frac{4\sqrt{3}}{\sqrt{3}}$=4.
∵四边形BECD是平行四边形,
∴BD=CE=4,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4$\sqrt{3}$×4=8$\sqrt{3}$.
点评 本题综合考查了菱形的性质,平行四边形的判定与性质以及解直角三角形.证明出四边形BECD是平行四边形是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
12.实数a,b,c,d在数轴上的对应点从左到右依次是A,B,C,D,若b+d=0,则a+c的值( )
| A. | 小于0 | B. | 等于0 | ||
| C. | 大于0 | D. | 与a,b,c,d的取值有关 |
13.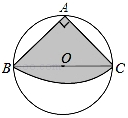 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
| A. | 12cm | B. | 20cm | C. | 24cm | D. | 28cm |
17.在实数-2,$\sqrt{2}$,0,-1中,最小的数是( )
| A. | -2 | B. | $\sqrt{2}$ | C. | 0 | D. | -1 |
7.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
则方程ax2+bx+2=0的根是( )
| … | 0 | 50 | 200 | … | |
| y | … | 1 | -1 | 1 | … |
| A. | x1=x2=100 | B. | x1=0,x2=200 | C. | x1=50,x2=150 | D. | x1=50,x2=250 |
11.估计$\frac{\sqrt{5}-1}{2}$介于( )
| A. | 0.6与0.7之间 | B. | 0.7与0.8之间 | C. | 0.8与0.9之间 | D. | 0.9与1之间 |
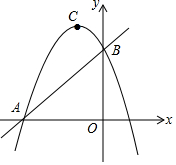 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.