题目内容
4.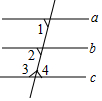 如图,下列推理错误的是( )
如图,下列推理错误的是( )| A. | ∵∠1=∠2,∴a∥b | B. | ∵b∥c,∴∠2=∠4 | ||
| C. | ∵a∥b,b∥c,∴a∥c | D. | ∵∠2+∠3=180°,∴a∥c |
分析 由平行线的判定与性质得出选项A、B、C正确,D错误;即可得出结论.
解答 解:∵∠1=∠2,∴a∥b,选项A正确;
∵b∥c,∴∠2=∠4,选项B正确;
∵a∥b,b∥c,∴a∥c,选项C正确;
∵∠2+∠3=180°,∴b∥c,选项D错误;
故选:D.
点评 本题考查了平行线的判定与性质、平行线公理;熟练掌握平行线的判定与性质是解决问题的关键.

练习册系列答案
相关题目
14.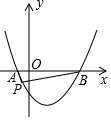 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
15. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )| A. | 48° | B. | 42° | C. | 40° | D. | 45° |
12.实数a,b,c,d在数轴上的对应点从左到右依次是A,B,C,D,若b+d=0,则a+c的值( )
| A. | 小于0 | B. | 等于0 | ||
| C. | 大于0 | D. | 与a,b,c,d的取值有关 |
19.一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 不可能事件 | D. | 以上都不是 |
9. 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )
 如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A、B、C、D、E的坐标分别是(0,a)、(-3,2)、(b,m)、(-b,m),则点E的坐标是( )| A. | (2,-3) | B. | (2,3) | C. | (3,2) | D. | (3,-2) |
13.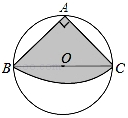 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
| A. | 12cm | B. | 20cm | C. | 24cm | D. | 28cm |
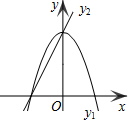 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: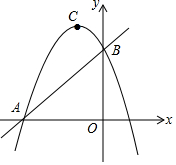 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.