题目内容
3. 如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.
如图,在正方形ABCD中,AB=4$\sqrt{2}$,AC与BD相交于点O,点P是AC上一动点,点E为射线BC上的一点,且PB=PE,过点E作EF⊥AC,垂足为点F.(1)当点F在线段AC上时,求PF=BO;
(2)设AP=x,△PBE的面积为y,求y与x之间的函数关系式,并写出自变量的取值范围;
(3)是否存在这样的P点,使得△PBE的面积是△ABC面积的$\frac{3}{8}$?如果存在,求出AP的长;如果不存在,请说明理由.
分析 (1)由正方形的性质得出BC=AB=4$\sqrt{2}$,AC⊥BD,∠ACB=∠CBD=45°,由等腰三角形的性质、三角形的外角性质求出∠FPE=∠OBP,由AAS证明△PEF≌△BPO,即可得出结论;
(2)作PG⊥BC于G,则PG∥AB,PG=CG,BG=EG,由平行线得出△PCG∽△ACB,得出对应边成比例求出CG=PG=4$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x,得出BG=BC-CG=$\frac{\sqrt{2}}{2}$x,BE=$\sqrt{2}$x,由三角形的面积公式即可得出答案;
(3)求出△ABC的面积=$\frac{1}{2}$×4$\sqrt{2}$÷$\sqrt{2}$=16,由△PBE的面积是△ABC面积的$\frac{3}{8}$得出方程,解方程即可.
解答 (1)证明:∵四边形ABCD是正方形,
∴BC=AB=4$\sqrt{2}$,AC⊥BD,∠ACB=∠CBD=45°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=8,
∵PB=PE,
∴∠PBE=∠PEB,
∵∠PBE=∠CBD+∠OBP,∠PEB=∠ACB+∠FPE,
∴∠FPE=∠OBP,
∵EF⊥AC,
∴∠PFE=∠BOP=90°,
在△PEF和△BPO中,$\left\{\begin{array}{l}{∠PFE=∠BOP}&{\;}\\{∠FPE=∠OBP}&{\;}\\{PE=PB}&{\;}\end{array}\right.$,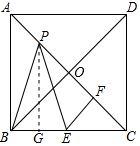
∴△PEF≌△BPO(AAS),
∴PF=BO;
(2)解:作PG⊥BC于G,如图所示:
则PG∥AB,PG=CG,BG=EG,
∴△PCG∽△ACB,
∴$\frac{PG}{AB}=\frac{PC}{AC}$,即$\frac{PG}{4\sqrt{2}}=\frac{8-x}{8}$,
∴CG=PG=4$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x,
∴BG=BC-CG=$\frac{\sqrt{2}}{2}$x,
∴BE=$\sqrt{2}$x,
∴△PBE的面积y=$\frac{1}{2}$BE•PG=$\frac{1}{2}$×$\sqrt{2}$x×(4$\sqrt{2}$-$\frac{\sqrt{2}}{2}$x),
即y=-$\frac{1}{2}$x2+4x(0<x<8);
(3)解:存在,理由如下:
△ABC的面积=$\frac{1}{2}$×4$\sqrt{2}$÷$\sqrt{2}$=16,
若△PBE的面积是△ABC面积的$\frac{3}{8}$,
则=-$\frac{1}{2}$x2+4x=$\frac{3}{8}$×16=6,
解得:x=2或x=6,
即AP的长为2或6.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰三角形的性质、相似三角形的判定与性质、三角形的面积的计算等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案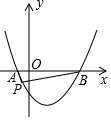 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )| A. | -1<m<0 | B. | -1<m<0或3<m<4 | C. | 0<m<3或m>4 | D. | m<-1或0<m<3 |
①一元二次方程ax2+4ax+m=0的两根为x1=-1,x2=-3
②原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,则CD=4
③点E(1,y1),点F(-3,y2)在原抛物线上,则y2>y1
④抛物线y=ax2-4ax+m与原抛物线关于y轴对称.
其中正确的是( )
| A. | ①②③④ | B. | ①②④ | C. | ①② | D. | ①②③ |
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=48°,则∠2的度数为( )| A. | 48° | B. | 42° | C. | 40° | D. | 45° |
| A. | 小于0 | B. | 等于0 | ||
| C. | 大于0 | D. | 与a,b,c,d的取值有关 |
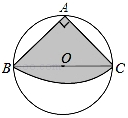 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
| A. | 12cm | B. | 20cm | C. | 24cm | D. | 28cm |
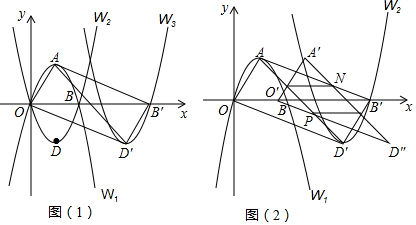
 如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.
如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.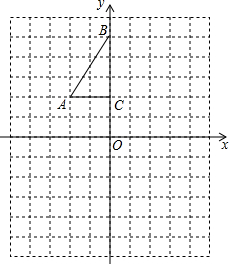 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).