题目内容
8. 如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )
如图,将一块直角三角板的直角顶点放在直尺的一边上.若∠2=40°,则∠1的度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
分析 由两直线平行,同位角相等,可求得∠3的度数,然后求得∠1的度数.
解答  解:如图,
解:如图,
∵∠2=50°,
∴∠3=∠2=40°,
∴∠1=90°-40°=50°.
故选B.
点评 此题考查了平行线的性质.注意两直线平行,同位角相等定理的应用是解此题的关键.

练习册系列答案
相关题目
19.一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 不可能事件 | D. | 以上都不是 |
3.已知正方体的体积为2$\sqrt{2}$,则这个正方体的棱长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3 |
13.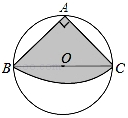 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
 如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,
如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为3$\sqrt{30}$cm,则这块圆形纸片的直径为( )
| A. | 12cm | B. | 20cm | C. | 24cm | D. | 28cm |
20.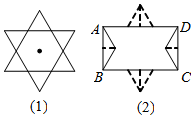 小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问
小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问
题:若将该矩形围成圆柱,则圆柱的高为( )
 小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问
小东同学对图形世界充满兴趣,他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°,旋转前后的两个正三角形构成如图(1)的一个六角星;然后将该六角星按图(2)分割后拼成矩形ABCD.请你思考小东的问题:若将该矩形围成圆柱,则圆柱的高为( )
| A. | 2$\sqrt{3}$cm | B. | 3$\sqrt{3}$cm | C. | 2$\sqrt{3}$cm 或6 cm | D. | 3cm或3$\sqrt{3}$cm |
17.在实数-2,$\sqrt{2}$,0,-1中,最小的数是( )
| A. | -2 | B. | $\sqrt{2}$ | C. | 0 | D. | -1 |
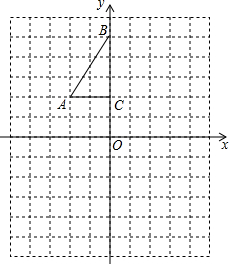 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点坐标分别为A(-2,2),B(0,5),C(0,2).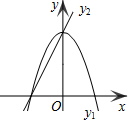 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断: