题目内容
19. 若平行四边形ABCD的面积为24cm2,则三角形ABO的面积为( )cm2.
若平行四边形ABCD的面积为24cm2,则三角形ABO的面积为( )cm2.| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 因为平行四边形的对角线互相平分,所以对角线分成的四个三角形的面积相等,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴S△ABO=S△DOC=S△AOD=S△BOC=$\frac{1}{4}$?ABCD的面积=$\frac{1}{4}$×24cm2=6cm2,
故选:B.
点评 此题主要考查平行四边形的性质、三角形的面积关系;熟练掌握平行四边形的对角线互相平分,熟记等(同)底等高的三角形的面积相等是解题的关键.

练习册系列答案
相关题目
7.在平面直角坐标系内,把点P(-5,-2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是( )
| A. | (-3,2) | B. | (-7,-6) | C. | (-7,2) | D. | (-3,-6) |
14. 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | AB2=AP•AC | D. | $\frac{AB}{BP}$=$\frac{AC}{CB}$ |
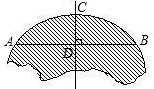 如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.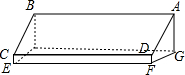 “蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数).
“蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数).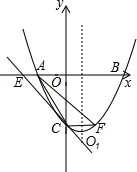 如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.