题目内容
19. 如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
分析 先由三角形的中位线定理推知四边形EFGH是平行四边形,然后由AC⊥BD可以证得平行四边形EFGH是矩形.
解答 证明:如图,∵E、F、G、H分别是线段AB、BC、CD、AD的中点,
∴EH、FG分别是△ABD、△BCD的中位线,EF、HG分别是△ACD、△ABC的中位线,
根据三角形的中位线的性质知,EF∥AC,GH∥AC且EF=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC
∴四边形EFGH是平行四边形
又∵AC⊥BD,
∴EF⊥FG
∴四边形EFGH是矩形.
点评 本题主要考查中点四边形,解题时,利用三角形中位线定理判定四边形EFGH是平行四边形是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
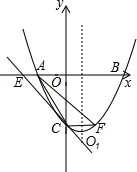 如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
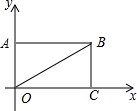 如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).
如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).