题目内容
4. 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )| A. | m=k | B. | m=h | C. | k>n | D. | h<0,n>0 |
分析 根据二次函数的图象的对称轴和与y轴的交点即可判断.
解答 解:由函数的图象可知:两条抛物线的对称轴相同,则x=m=h,故B错误;
抛物线y=$\frac{1}{2}$(x-m)2+n与y轴的解得在抛物线y=$\frac{1}{4}$(x-h)2+k的下方,则k>n,故C错误;
∵对称轴在x轴的左侧,与y的交点在y轴的正半轴,∴h<0,m<0,k>0n>0,故A正确,D错误;
故选A,
点评 本题考查了二次函数的性质,由图看出抛物线的顶点和与y轴的交点的位置关系同函数关系式中数值的关系.本题为非常基础的二次函数性质的应用题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14. 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
 如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )
如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | AB2=AP•AC | D. | $\frac{AB}{BP}$=$\frac{AC}{CB}$ |
19.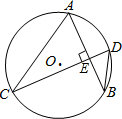 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
16. 如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
 如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,1) | D. | (4,1) |
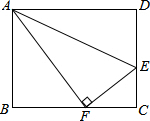 如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$.
如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE翻折,点D的对称点F恰好落在BC上,已知AD=20cm,AB=16cm,那么折痕AE的长为10$\sqrt{5}$. 如图,菱形ABCD的边长为5,以菱形ABCD的对称中心为原点O,平行于AD的直线为x轴建立平面直角坐标系,已知A(-1,2),点D在双曲线y=$\frac{k}{x}$上.
如图,菱形ABCD的边长为5,以菱形ABCD的对称中心为原点O,平行于AD的直线为x轴建立平面直角坐标系,已知A(-1,2),点D在双曲线y=$\frac{k}{x}$上.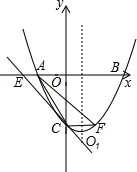 如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.