题目内容
7．
如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，若S△DEF=3，则S△BCF为（ ）| A． | 6 | B． | 9 | C． | 12 | D． | 10 |
分析 根据平行四边形的性质得到AD∥BC和△EFD∽△CFB，根据相似三角形的面积比是相似比的平方得到答案．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴△EFD∽△CFB，
∵E是边AD的中点，
∴DE=$\frac{1}{2}$BC，
∴S△DEF：S△BCF=1：4，
∵S△DEF=3，
∴S△BCF=12，
故选C．
点评 本题考查的是平行四边形的性质和相似三角形的判定和性质，掌握三角形相似的判定定理和性质定理是解题的关键，注意：相似三角形的面积比是相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
15．已知一次函数y=-$\frac{1}{2}$x+2，当1≤x≤4时，y的最大值是（ ）
| A． | 2 | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | -6 |
2．新年来临之际，某班同学向班上其他同学互赠新年贺卡，全班共互赠贺卡2980张，设全班有x名学生，那么根据题意可列方程（ ）
| A． | x（x+1）=2980 | B． | $\frac{1}{2}$x（x-1）=2980 | C． | x（x-1）=2980 | D． | $\frac{1}{2}$x（x+1）=2980 |
12．计算-42的结果等于（ ）
| A． | -16 | B． | 16 | C． | -8 | D． | 8 |
16．将抛物线y=x2+4x+3沿y轴向右平移3个单位，然后再向上平移5个单位后所得抛物线的顶点坐标是（ ）
| A． | （5，7） | B． | （-1，7） | C． | （1，4） | D． | （5，4） |
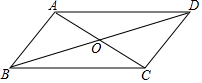在?ABCD中，对角线AC，BD相交于点O，若AB=4，BD=10，sin∠BDC=$\frac{3}{5}$，则?ABCD的面积是24．