题目内容
17.图①为平地上一幢建筑物与铁塔图,图②为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=20m,在A点测得D点的俯角为45°,测得C点的仰角为58°.求铁塔CD的高度.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)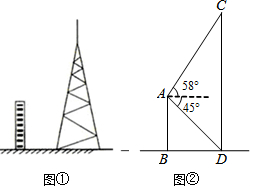
分析 先过点A作AE⊥CD,垂足为E,则四边形ABDE矩形,根据∠ADB=∠EAD=45°,可得AB=ED=BD=20m,在Rt△AEC中,根据tan∠CAE=$\frac{CE}{AE}$,求得CE的长,进而得到铁塔CD的高度.
解答  解:如图,过点A作AE⊥CD,垂足为E,则四边形ABDE矩形,
解:如图,过点A作AE⊥CD,垂足为E,则四边形ABDE矩形,
∵BD=20m,在A点测得D点的俯角为45°,在测得C点的仰角为58°,
∴∠ADB=∠EAD=45°,
∴AB=ED=BD=20m,
在Rt△AEC中,tan∠CAE=$\frac{CE}{AE}$,
∴tan58°=$\frac{CE}{AE}$=$\frac{CE}{20}$,
∴CE=20 tan58°=20×1.60=32,
∴CD=CE+ED=32+20=52米.
答:铁塔CD的高度为52米.
点评 本题主要考查了解直角三角形的应用,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
7.我市某一周的日最高气温统计如下表:
则这周日最高气温的中位数是27℃.
| 最高气温(℃) | 25 | 26 | 27 | 28 |
| 天数(天) | 1 | 1 | 2 | 3 |
8.为了解某校初二学生每周上网的时间,两位学生进行了抽样调查,小丽调查了初二电脑爱好者中40名学生每周上网的时间:小杰从全校400初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如表所示.
(1)你认为哪位同学抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
| 时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
| 0~1 | 6 | 22 |
| 1~2 | 10 | 10 |
| 2~3 | 16 | 6 |
| 3~4 | 8 | 2 |
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
12.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
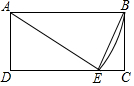 如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.
如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.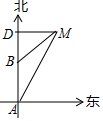 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).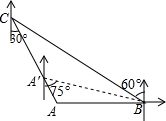 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )