题目内容
19.计算:3cos60°-2-1+(π-3)0-$\sqrt{(-2)^{2}}$.分析 直接利用负指数幂的性质以及零指数幂的性质和二次根式的性质、特殊角的三角函数值分别化简求出答案.
解答 解:原式=3×$\frac{1}{2}$-$\frac{1}{2}$+1-2
=0.
点评 此题主要考查了负指数幂的性质以及零指数幂的性质和二次根式的性质、特殊角的三角函数值,正确化简各数是解题关键.

练习册系列答案
相关题目
10. 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
4.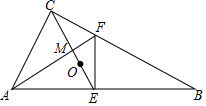 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.把抛物线y=-x2向左平移2个单位,再向上平移3个单位,平移后的抛物线的解析式为( )
| A. | y=-(x-2)2-3 | B. | y=-(x+2)2-3 | C. | y=-(x+2)2+3 | D. | y=-(x-2)2+3 |
9.甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
| 平均数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 2 |
| 乙 | 8 | 8 | 2.2 |
| 丙 | 6 | 6 | 3 |
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
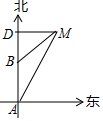 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°). 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( ) 如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )
如图是由3个相同的正方体组成的一个立方体图形,它的三视图是( )



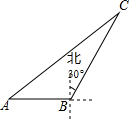 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.