题目内容
17.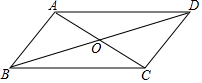 在?ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=$\frac{3}{5}$,则?ABCD的面积是24.
在?ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC=$\frac{3}{5}$,则?ABCD的面积是24.
分析 作OE⊥CD于E,由平行四边形的性质得出OA=OC,OB=OD=$\frac{1}{2}$BD=5,CD=AB=4,由sin∠BDC=$\frac{3}{5}$,证出AC⊥CD,OC=3,AC=2OC=6,得出?ABCD的面积=CD•AC=24.
解答 解:作OE⊥CD于E,如图所示: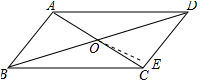
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD=$\frac{1}{2}$BD=5,CD=AB=4,
∵sin∠BDC=$\frac{OE}{OD}$=$\frac{3}{5}$,
∴OE=3,
∴DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=4,
∵CD=4,
∴点E与点C重合,
∴AC⊥CD,OC=3,
∴AC=2OC=6,
∴?ABCD的面积=CD•AC=4×6=24;
故答案为:24.
点评 本题考查了平行四边形的性质、三角函数、勾股定理等知识;熟练掌握平行四边形的性质,得出AC⊥CD是关键

练习册系列答案
相关题目
2.截至2016年底,国家开发银行对“一带一路”沿线国家累计发放贷款超过1600亿美元,其中1600亿用科学记数法表示为( )
| A. | 16×1010 | B. | 1.6×1010 | C. | 1.6×1011 | D. | 0.16×1012 |
9.甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
甲:9,10,8,5,7,8,10,8,8,7
乙:5,7,8,7,8,9,7,9,10,10
丙:7,6,8,5,4,7,6,3,9,5
(1)根据以上数据完成下表:
| 平均数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 2 |
| 乙 | 8 | 8 | 2.2 |
| 丙 | 6 | 6 | 3 |
(3)比赛时三人依次出场,顺序由抽签方式决定,求甲、乙相邻出场的概率.
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )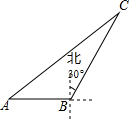 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.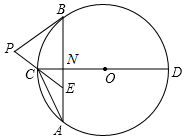 如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE
如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE