题目内容
16.将抛物线y=x2+4x+3沿y轴向右平移3个单位,然后再向上平移5个单位后所得抛物线的顶点坐标是( )| A. | (5,7) | B. | (-1,7) | C. | (1,4) | D. | (5,4) |
分析 利用平移可求得平移后的抛物线的解析式,可求得其顶点坐标.
解答 解:∵y=x2+4x+3=(x+2)2-1,
∴先向右平移3个单位长度,再向上平移5个单位长度后抛物线解析式为y=(x-1)2+4,
∴顶点坐标为(1,4),
故选C.
点评 本题主要考查函数图象的平移,求得平移后抛物线的解析式是解题的关键.

练习册系列答案
相关题目
4.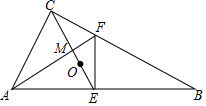 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.把抛物线y=-x2向左平移2个单位,再向上平移3个单位,平移后的抛物线的解析式为( )
| A. | y=-(x-2)2-3 | B. | y=-(x+2)2-3 | C. | y=-(x+2)2+3 | D. | y=-(x-2)2+3 |
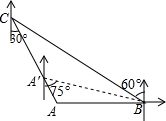 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )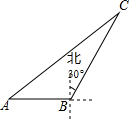 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.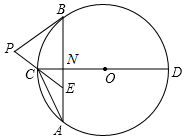 如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE
如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE