题目内容
18.已知:线段CB=6,点A在线段BC上,且CA=2,以AB为直径做半圆O,点D为半圆O上的动点,以CD为边向外作等边△CDE.发现:CD的最小值是2,最大值是6,△CBD面积的最大值是6.
思考:如图1,当线段CD所在直线与半圆O相切时,求弧BD的长.
探究:如图2,当线段CD与半圆O有两个公共点D,M时,若CM=DM,求等边△CDE面积.

分析 发现:根据圆的性质、三角形的面积公式计算;
思考:连接OD,根据切线的性质得到OD⊥CD,根据直角三角形的性质求出∠C,得到∠BOD,根据弧长公式计算即可;
探究:根据切割线定理求出CD,根据等边三角形的面积公式计算即可.
解答 解:发现:当点D与点A重合时,CD最小,CD的最小值是2,
当点D与点B重合时,CD最大,CD的最大值是6,
当OD⊥CB时,CD最小,△CBD的面积最大,最大值为:$\frac{1}{2}$×6×2=6,
故答案为:2;6;6;
思考:连接OD,
∵线段CD所在直线与半圆O相切,
∴OD⊥CD,
∵OC=4,OD=2,
∴∠C=30°,
∴∠COD=60°,
∴∠BOD=120°,
∴弧BD的长为:$\frac{120π×2}{180}$=$\frac{4}{3}$π;
探究:∵CM=DM,
∴CD=2CM,
由切割线定理得,CM•CD=CA•CB=12,
解得,CM=$\sqrt{6}$,
则CD=2$\sqrt{6}$,
∴等边△CDE面积为:$\frac{1}{2}$×2$\sqrt{6}$×2$\sqrt{6}$×sin60°=6$\sqrt{3}$.
点评 本题考查的是切线的性质、弧长的计算、切割线定理的应用,作为弧长的计算公式、切线的性质是解题的关键.

练习册系列答案
相关题目
8.为了解某校初二学生每周上网的时间,两位学生进行了抽样调查,小丽调查了初二电脑爱好者中40名学生每周上网的时间:小杰从全校400初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如表所示.
(1)你认为哪位同学抽取的样本不合理?请说明理由.
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
| 时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
| 0~1 | 6 | 22 |
| 1~2 | 10 | 10 |
| 2~3 | 16 | 6 |
| 3~4 | 8 | 2 |
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?
10. 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
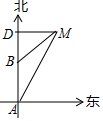 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).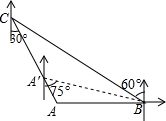 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里. 2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离.
2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )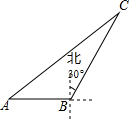 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.