题目内容
15.已知一次函数y=-$\frac{1}{2}$x+2,当1≤x≤4时,y的最大值是( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | -6 |
分析 根据一次函数的系数k=-$\frac{1}{2}$,可得出y随x值的增大而减小,将x=1代入一次函数解析式中求出y值即可.
解答 解:在一次函数y=-$\frac{1}{2}$x+2中k=-$\frac{1}{2}$<0,
∴y随x值的增大而减小,
∴当x=1时,y取最大值,最大值为-$\frac{1}{2}$×1+2=$\frac{3}{2}$.
故选B.
点评 本题考查了一次函数的性质,牢记“k<0,y随x的增大而减小”是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
10. 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
 如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )
如图,直线a∥b,c⊥d,若∠α=35°,则∠β=( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
20.若二次函数y=2x2-2mx+2m-2的图象的顶点在x轴上,则m的值是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±1 |
4.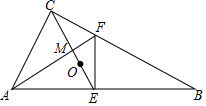 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
 如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )
如图,直角△ABC中,∠B=30°,点O是△ABC的重心,连接CO并延长交AB于点E,过点E作EF⊥AB交BC于点F,连接AF交CE于点M,则$\frac{MO}{MF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
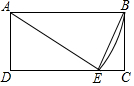 如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.
如图,矩形ABCD中,AB=10,AD=6,以A为圆心,AB为半径作圆弧交CD于E,连结EA,EB.则tan∠AEB的值为3.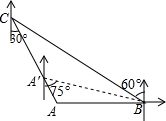 如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里.
如图,“中海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛瞧C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距150海里. 2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离.
2016年11月1日至6日,第十一届中国航展在广东珠海举行.在本次航展上,一架飞机飞行到A点时,测得观礼台C在飞机前下方,俯角为65°,此时飞机飞行路线改为沿坡脚30°的方向朝斜上方直线飞行,飞机飞行6km到达B处,此时飞机飞行高度为5km,另一个观礼台D恰好在飞机的正下方,求两个观礼台C与D之间的距离. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=3,则S△BCF为( )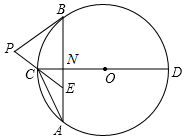 如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE
如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE