题目内容
已知方程x2+2ax+a-4=0有两个不同的实数根,方程x2+2ax+k=0也有两个不同的实数根,且其两根介于方程x2+2ax+a-4=0的两根之间,求k的取值范围.
考点:抛物线与x轴的交点,根的判别式
专题:
分析:由方程x2+2ax+a-4=0恒有相异两实根,则△>0,而△=4a2-4(a-4)=4(a2-a+4)=4[(a-
)2+
],得a为任意实数,由方程x2+2ax+k=0也有相异两实根,△′=4a2-4k>0,即k<a2;并且它的两根介于上面方程的两根之间,可利用二次函数的图象继续求k的范围.
| 1 |
| 2 |
| 15 |
| 4 |
解答: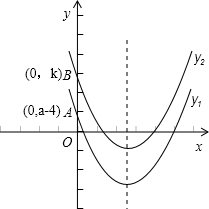 解:∵方程x2+2ax+a-4=0有两个不同的实数根
解:∵方程x2+2ax+a-4=0有两个不同的实数根
∴△>0,而△=4a2-4(a-4)=4(a-
)2+15≥15.
又∵方程x2+2ax+k=0也有两个不同的实数根
∴△′=4a2-4k>0,即k<a2
对于二次函数y1=x2+2ax+a-4和y2=x2+2ax+k,它们的对称轴相同,且与x轴都有两个不同的交点
∵y2与x轴的两个交点都在y1与x轴的两个交点之间
∴y2与y轴的交点在y1与y轴的交点上方,如图,∴k>a-4,
∴k的取值范围是:a-4<k<a2.
 解:∵方程x2+2ax+a-4=0有两个不同的实数根
解:∵方程x2+2ax+a-4=0有两个不同的实数根∴△>0,而△=4a2-4(a-4)=4(a-
| 1 |
| 2 |
又∵方程x2+2ax+k=0也有两个不同的实数根
∴△′=4a2-4k>0,即k<a2
对于二次函数y1=x2+2ax+a-4和y2=x2+2ax+k,它们的对称轴相同,且与x轴都有两个不同的交点
∵y2与x轴的两个交点都在y1与x轴的两个交点之间
∴y2与y轴的交点在y1与y轴的交点上方,如图,∴k>a-4,
∴k的取值范围是:a-4<k<a2.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了运用二次函数图象解决不等式的问题.

练习册系列答案
相关题目
方程x2-2x+6=0的根的情况为( )
| A、有两个不等的实数根 |
| B、有两个相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |
 已知二次函数图象的顶点是(-1,2),且过点(0,
已知二次函数图象的顶点是(-1,2),且过点(0, 如图,梯形ABCD中,AB∥CD,∠ABC和∠BCD的平分线的交点E在AD上.
如图,梯形ABCD中,AB∥CD,∠ABC和∠BCD的平分线的交点E在AD上. 如图,△ABC的内切圆分别切BC,CA、AB三边于D、E、F,M是EF上一点,且DM⊥EF,求证:DM平分∠BMC.
如图,△ABC的内切圆分别切BC,CA、AB三边于D、E、F,M是EF上一点,且DM⊥EF,求证:DM平分∠BMC. 如图,在∠AOB外有一点P,先作点P关于直线OA的对称点P1,再作点P关于直线OB的对称点P2.
如图,在∠AOB外有一点P,先作点P关于直线OA的对称点P1,再作点P关于直线OB的对称点P2.