题目内容
13. 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在$\widehat{EF}$上,设∠BDF=a(0<a≤90°).当a由小到大变化时,图中阴影部分的面积π-2.
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在$\widehat{EF}$上,设∠BDF=a(0<a≤90°).当a由小到大变化时,图中阴影部分的面积π-2.
分析 作DM⊥AC于M,DN⊥BC于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积-正方形DMCN的面积,即可得出结果.
解答 解:作DM⊥AC于M,DN⊥BC于N,连接DC,如图所示:
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{4}$AB,DN=$\frac{\sqrt{2}}{2}$BD=$\frac{\sqrt{2}}{4}$AB,
∴DM=DN,
∴四边形DMCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°-∠GDN,
∵∠EDF=90°,
∴∠NDH=90°-∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
$\left\{\begin{array}{l}{∠MDG=∠NDH}\\{∠DMG=∠DNH}\\{DM=DN}\end{array}\right.$,
∴△DMG≌△DNH(AAS),
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=$\frac{1}{8}$AB2,=$\frac{1}{8}$×42=2,
∴四边形DGCH的面积=$\frac{1}{8}$AB2,
∵扇形FDE的面积=$\frac{90π•C{D}^{2}}{360}=\frac{πA{B}^{2}}{16}=\frac{π×{4}^{2}}{16}$=π,
∴阴影部分的面积=扇形面积-四边形DGCH的面积=π-2.
故答案为:π-2.
点评 本题主要考查了等腰直角三角形斜边中线的性质,正方形的性质,全等三角形的判定和性质,能正确作出辅助线构造全等三角形是解题的关键.

 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.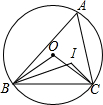 如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.
如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°. 如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).
如图,点P是⊙O外一点,请用尺规过点P作⊙O的切线PA,切点为A(不写画法,保留作图痕迹).