题目内容
1. 已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;
(2)若DE=3cm,AE=1cm,求⊙O的半径.
分析 (1)连接OD,根据平行线的判断方法与性质可得∠ODE=∠DEM=90°,且D在⊙O上,故DE是⊙O的切线.
(2)由直角三角形的特殊性质,可得AD的长,又有△ACD∽△ADE.根据相似三角形的性质列出比例式,代入数据即可求得圆的半径.
解答 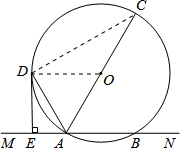 (1)证明:连接OD.
(1)证明:连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠OAD=∠DAE,
∴∠ODA=∠DAE.
∴DO∥MN.
∵DE⊥MN,
∴∠ODE=∠DEM=90°.
即OD⊥DE.
∵D在⊙O上,OD为⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵∠AED=90°,DE=3cm,AE=1cm,
∴AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{10}$.
连接CD.
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.
∵∠CAD=∠DAE,
∴△ACD∽△ADE.
∴$\frac{AD}{AE}$=$\frac{AC}{AD}$.
∴$\frac{\sqrt{10}}{1}$=$\frac{AC}{\sqrt{10}}$.
则AC=10(cm).
∴⊙O的半径是5cm.
点评 本题考查圆的切线的判定、直径的性质、勾股定理切割线定理、相似三角形的判定和性质等知识,在圆中学会正确添加辅助线是解决问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
5.下列图案中,既是中心对称图形又是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
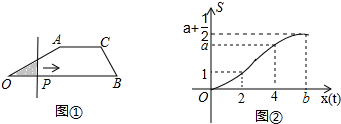
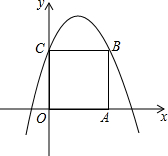 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$. 如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在$\widehat{EF}$上,设∠BDF=a(0<a≤90°).当a由小到大变化时,图中阴影部分的面积π-2.
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在$\widehat{EF}$上,设∠BDF=a(0<a≤90°).当a由小到大变化时,图中阴影部分的面积π-2.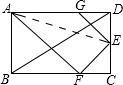 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.