题目内容
1.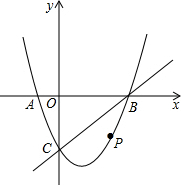 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.(1)求A、B、C三点坐标;
(2)当点P运动到什么位置时,CP∥AB,且AC=BP,直接写出此时P点的坐标:P(2,-3)
(3)连接PO、PC,并把抛物线沿CO翻折,此时,可得到四边形POP'C,那么,是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
分析 (1)根据二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,从而可以求得A、B、C三点坐标;
(2)根据二次函数的图象具有对称性,由点C的坐标和对称轴即可得到点P的坐标;
(3)根据菱形的性质和二次函数图象上点的特征,翻折的性质即可求得使四边形POP'C为菱形的点P的坐标.
解答 解:(1)∵y=x2-2x-3,
∴当y=0时,0=x2-2x-3,得x1=-1,x2=3,
当x=0时,y=-3,
∴点A的坐标为(-1,0),点B的坐标为(3,0),点C的坐标为(0,-3);
(2)∵CP∥AB,且AC=BP,点C(0,-3),y=x2-2x-3=(x-1)2-4,
∴抛物线的对称轴为直线x=1,
∴点P的坐标为(2,-3),
故答案为:(2,-3);
(3)存在点P,使四边形POP'C为菱形,
∵四边形POP'C为菱形,
∴PP′⊥OC,且PP′平分OC,
∵点O(0,0),点C(0,-3),
∴点P的纵坐标为y=-1.5,
将y=-1.5代入y=x2-2x-3,得
-1.5=x2-2x-3,
解得,x1=$1+\frac{\sqrt{10}}{2}$,x2=$1-\frac{\sqrt{10}}{2}$,
即点P的坐标为($1+\frac{\sqrt{10}}{2},-1.5$)或($1-\frac{\sqrt{10}}{2},-1.5$).
点评 本题考查二次函数综合题、菱形的性质、翻折的性质,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用数形结合和二次函数以及翻折的性质解答.

练习册系列答案
相关题目
16.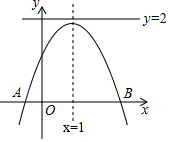 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0)和B(3,0).下列结论中:①abc>0;②2a+b=0;③方程ax2+bx+c=2(a≠0)没有实数根.其中正确的结论有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0)和B(3,0).下列结论中:①abc>0;②2a+b=0;③方程ax2+bx+c=2(a≠0)没有实数根.其中正确的结论有( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0)和B(3,0).下列结论中:①abc>0;②2a+b=0;③方程ax2+bx+c=2(a≠0)没有实数根.其中正确的结论有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0)和B(3,0).下列结论中:①abc>0;②2a+b=0;③方程ax2+bx+c=2(a≠0)没有实数根.其中正确的结论有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
13.射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
(1)完成表中填空①9;②9;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为$\frac{4}{3}$,你认为推荐谁参加比赛更合适,请说明理由.
(注:方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为$\frac{4}{3}$,你认为推荐谁参加比赛更合适,请说明理由.
(注:方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
11.将圆心角为90°,面积为4π的扇形围成一个圆锥的一个侧面,所围成圆锥的底面半径为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
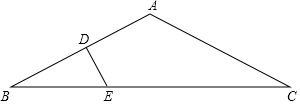 如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.
如图,△ABC中,AB=AC=2$\sqrt{5}$,BC=8,AB的垂直平分线交AB于点D,交BC于点E,设△BDE的面积为S1,四边形ADEC的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{5}{27}$.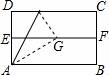 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为60°.
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为60°. 请在网格坐标系中画出二次函数y=x2-4x+1的大致图象(注:图中小正方形网格的边长为1),根据图象填空:
请在网格坐标系中画出二次函数y=x2-4x+1的大致图象(注:图中小正方形网格的边长为1),根据图象填空: