题目内容
13.射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩的方差为$\frac{4}{3}$,你认为推荐谁参加比赛更合适,请说明理由.
(注:方差公式s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2])
分析 (1)根据中位数的定义先把这组数据从小到大排列,再找出最中间两个数的平均数即可求出①;根据平均数的计算公式即可求出②;
(2)根据方差的计算公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],代值计算即可;
(3)根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,即可得出答案.
解答 解:(1)甲的中位数是:$\frac{9+9}{2}$=9;
乙的平均数是:(10+7+10+10+9+8)÷6=9;
故答案为:9,9;
(2)S甲2=$\frac{1}{6}$[(10-9)2+(8-9)2+(9-9)2+(8-9)2+(10-9)2+(9-9)2]=$\frac{2}{3}$;
(3)∵$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,S甲2<S乙2,
∴推荐甲参加比赛合适.
点评 本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
3.在-$\sqrt{(-5)^{2}}$,2π,$\sqrt{0.4}$,$\frac{1}{7}$,0中无理数个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列说法中正确的是( )
| A. | 单项式x的系数和次数都是零 | B. | 34x3是7次单项式 | ||
| C. | a2b3的系数是5 | D. | 0是单项式 |
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.
如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.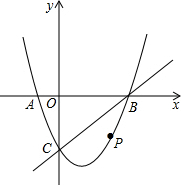 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.