题目内容
9.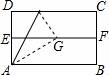 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为60°.
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为60°.
分析 直接利用翻折变换的性质以及直角三角形的性质得出∠2=∠4,再利用平行线的性质得出∠1=∠2=∠3,进而得出答案.
解答 解:如图所示:
由题意可得:∠1=∠2,AN=MN,∠MGA=90°,
则NG=$\frac{1}{2}$AM,故AN=NG,
则∠2=∠4,
∵EF∥AB,
∴∠4=∠3,
∴∠1=∠2=∠3=$\frac{1}{3}$×90°=30°,
∴∠DAG=60°,
故答案为:60°.
点评 此题主要考查了翻折变换的性质以及平行线的性质,正确得出∠2=∠4是解题关键.

练习册系列答案
相关题目
19.在如图所示的3×3方阵图中,处于同一横行、同一竖列、同一斜对角线上的3个数之和都相等.现在方阵图
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
中已填写了一些数和代数式(其中每个代数式都表示一个数),则x的值为-1,空白处应填写的3个数的和为-4.
| -2 | -4 | 3x+6 |
| 4 | x | |
| -x-6 |
14.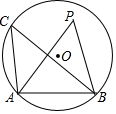 如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
 如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )
如图,AB是⊙O的弦,点C在⊙O上,∠ACB=40°,点P在⊙O的内部,且点C、点P在AB同侧,则∠APB的角度是( )| A. | 大于40° | B. | 等于40° | C. | 小于40° | D. | 无法确定 |
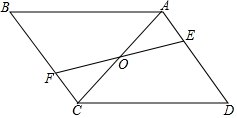 已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O.
已知:如图,平行四边形 ABCD中,点E、F分别在AD、BC上,且ED=BF,EF与AC相交于点O. 如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.
如图,AB∥CD,∠AEB=∠DFC,BF=CE,求证:△ABE≌△DCF.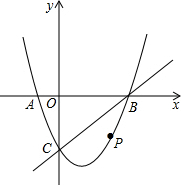 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.