题目内容
11.将圆心角为90°,面积为4π的扇形围成一个圆锥的一个侧面,所围成圆锥的底面半径为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先利用扇形的面积公式计算出扇形的半径为4,再设圆锥的底面半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和扇形面积公式得到$\frac{1}{2}$•2πr•4=4π,然后解此方程即可.
解答 解:设扇形的半径为R,则
$\frac{90•π•{R}^{2}}{360}$=4π,
解得R=4,
设圆锥的底面半径为r,
根据题意得$\frac{1}{2}$•2πr•4=4π,
解得r=1,
即圆锥的底面半径为1.
故选:A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.已知点A到直线BC的距离是4厘米,那么以点A为圆心4厘米为半径的圆与直线BC的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
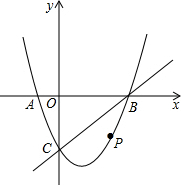 如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.
如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A、B两点,A点在原点的左侧,B点在原点右侧,与y轴交于C点,点P是x轴下方的抛物线上的一动点.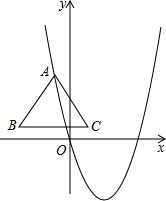 如图,已知等边三角形ABC的边长为$2\sqrt{3}$,它的顶点A在抛物线y=x2-2$\sqrt{3}$x上运动,且始终使BC∥x轴.
如图,已知等边三角形ABC的边长为$2\sqrt{3}$,它的顶点A在抛物线y=x2-2$\sqrt{3}$x上运动,且始终使BC∥x轴.